


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 18-12-2018
Date: 1-11-2018
Date: 24-10-2018
|
Let ![[arg(f(z))]](http://mathworld.wolfram.com/images/equations/VariationofArgument/Inline1.gif) denote the change in the complex argument of a function
denote the change in the complex argument of a function 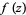 around a contour
around a contour 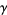 . Also let
. Also let 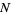 denote the number of roots of
denote the number of roots of 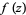 in
in 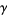 and
and 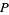 denote the sum of the orders of all poles of
denote the sum of the orders of all poles of 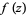 lying inside
lying inside 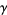 . Then
. Then
![[arg(f(z))]=2pi(N-P).](http://mathworld.wolfram.com/images/equations/VariationofArgument/NumberedEquation1.gif) |
(1) |
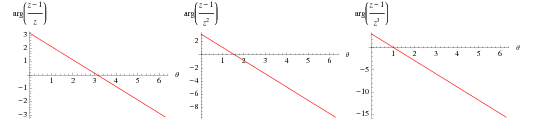
For example, the plots above shows the argument for a small circular contour 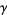 centered around
centered around 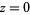 for a function of the form
for a function of the form 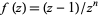 (which has a single pole of order
(which has a single pole of order 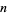 and no roots in
and no roots in 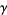 ) for
) for 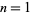 , 2, and 3.
, 2, and 3.
Note that the complex argument must change continuously, so any "jumps" that occur as the contour crosses branch cuts must be taken into account.
To find ![[arg(f(z))]](http://mathworld.wolfram.com/images/equations/VariationofArgument/Inline16.gif) in a given region
in a given region 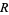 , break
, break 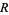 into paths and find
into paths and find ![[arg(f(z))]](http://mathworld.wolfram.com/images/equations/VariationofArgument/Inline19.gif) for each path. On a circular arc
for each path. On a circular arc
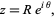 |
(2) |
let 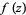 be a polynomial
be a polynomial 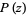 of degree
of degree 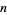 . Then
. Then
![[argP(z)]](http://mathworld.wolfram.com/images/equations/VariationofArgument/Inline23.gif) |
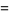 |
![[arg(z^n(P(z))/(z^n))]](http://mathworld.wolfram.com/images/equations/VariationofArgument/Inline25.gif) |
(3) |
 |
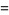 |
![[arg(z^n)]+[arg((P(z))/(z^n))].](http://mathworld.wolfram.com/images/equations/VariationofArgument/Inline28.gif) |
(4) |
Plugging in 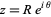 gives
gives
![[arg(P(z))]=[arg(Re^(ithetan))]+[arg((P(Re^(itheta)))/(Re^(ithetan)))].](http://mathworld.wolfram.com/images/equations/VariationofArgument/NumberedEquation3.gif) |
(5) |
So as 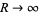 ,
,
![lim_(R->infty)(P(Re^(itheta)))/(Re^(ithetan))=[constant]](http://mathworld.wolfram.com/images/equations/VariationofArgument/NumberedEquation4.gif) |
(6) |
![[(P(Re^(itheta)))/(Re^(ithetan))]=0,](http://mathworld.wolfram.com/images/equations/VariationofArgument/NumberedEquation5.gif) |
(7) |
and
![[arg(P(z))]=[arg(e^(ithetan))]=n(theta_2-theta_1).](http://mathworld.wolfram.com/images/equations/VariationofArgument/NumberedEquation6.gif) |
(8) |
For a real segment 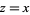 ,
,
![[arg(f(x))]=tan^(-1)[0/(f(x))]=0.](http://mathworld.wolfram.com/images/equations/VariationofArgument/NumberedEquation7.gif) |
(9) |
For an imaginary segment 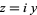 ,
,
![[arg(f(iy))]={tan^(-1)(I[P(iy)])/(R[P(iy)])}_(theta_1)^(theta_2).](http://mathworld.wolfram.com/images/equations/VariationofArgument/NumberedEquation8.gif) |
(10) |
REFERENCES:
Barnard, R. W.; Dayawansa, W.; Pearce, K.; and Weinberg, D. "Polynomials with Nonnegative Coefficients." Proc. Amer. Math. Soc. 113, 77-83, 1991.



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|