Polynomial Factorization
المؤلف:
Lenstra, A. K.; Lenstra, H. W.; and Lovász
المصدر:
"Factoring Polynomials with Rational Coefficients." Math. Ann. 261
الجزء والصفحة:
...
13-2-2019
2799
Polynomial Factorization
A factor of a polynomial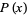 
of degree 
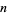is a polynomial 
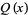of degree less than 
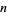which can be multiplied by another polynomial 
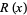of degree less than 
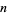to yield 
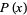, i.e., a polynomial 
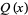such that
For example, since
both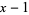 
and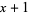 
are factors of 
.
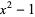Polynomial factorization can be performed in the Wolfram Language using Factor[poly]. Factorization over an algebraic number field is implemented as Factor[poly, Extension -> ext].
The coefficients of factor polynomials are often required to be real numbers or integers but could, in general, be complex numbers. The fundamental theorem of algebra states that a polynomial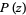 
of degree 
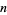has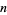 
values 
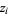(some of which are possibly degenerate) for which 
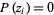. Such values are called polynomial roots.
The average number of factors of a polynomial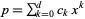 
of degree 
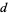with integer coefficients 
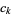in the range
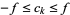has been considered by Schinzel (1976), Pinner and Vaaler (1996), Bérczes and Hajdu (1998), and Dubickas (1999).
REFERENCES:
Abbott, J.; Shoup, V.; and Zimmermann, P. "Factorization in ![Z[x]](http://mathworld.wolfram.com/images/equations/PolynomialFactorization/Inline21.gif)
: The Searching Phase." In Proceedings of the 2000 international Symposium on Symbolic and Algebraic Computation (St. Andrews, Scotland) (Ed. C. Traverso). New York: ACM, pp. 1-7, 2000.
Bérczes, A. and Hajdu, L. "On a Problem of P. Turán Concerning Irreducible Polynomials." In Number Theory. Diophantine, Computational and Algebraic Aspects. Proceedings of the International Conference held in Eger, July 29-August 2, 1996. (Ed. K. Győry, A. Pethő, and V. T. Sós). Berlin: de Gruyter, pp. 95-100, 1998.
Dubickas, A. "On a Polynomial with Large Number [sic] of Irreducible Factors." In Number theory in progress, Vol. 1. Diophantine Problems and Polynomials. Proceedings of the International Conference on Number Theory held in Honor of Andrzej Schinzel on his 60th Birthday in Zakopane-Kościelisko, June 30-July 9, 1997 (Ed. K. Győry, H. Iwaniec, and J. Urbanowicz). Berlin: de Gruyter, pp. 103-110, 1999.
Kaltofen, E. "Polynomial Factorization." In Computer Algebra: Symbolic and Algebraic Computation, 2nd ed. (Ed. B. Buchberger, G. E.Collins, R. Loos, and R. Albrecht). Vienna: Springer-Verlag, pp. 95-113, 1983.
Lenstra, A. K.; Lenstra, H. W.; and Lovász, L. "Factoring Polynomials with Rational Coefficients." Math. Ann. 261, 515-534, 1982.
Pinner, C. G. and Vaaler, J. D. "The Number of Irreducible Factors of a Polynomial. II." Acta Arith. 78, 125-142, 1996.
Schinzel, A. "On the Number of Irreducible Factors of a Polynomial." In Topics in Number Theory. Proceedings of the Colloquium held in Debrecen from 3-7 October, 1974. (Ed. P. Turán). Amsterdam, Netherlands: North Holland, pp. 305-314, 1976.
Séroul, R. "Factoring a Polynomial with Integral Coefficients." §10.14 in Programming for Mathematicians. Berlin: Springer-Verlag, pp. 286-295, 2000.
Trott, M. The Mathematica GuideBook for Symbolics. New York: Springer-Verlag, 2006. http://www.mathematicaguidebooks.org/.
van Hoeij, M. "Factoring Polynomials and the Knapsack Problem." Preprint.http://www.math.fsu.edu/~aluffi/archive/paper124.ps.gz.
الاكثر قراءة في مواضيع عامة في الجبر
اخر الاخبار
اخبار العتبة العباسية المقدسة
