المرجع الالكتروني للمعلوماتية
المرجع الألكتروني للمعلوماتية
ENGLISH
آخر المواضيع المضافة

الرياضيات
عدد المواضيع في هذا القسم 9761 موضوعاً
تاريخ الرياضيات
الرياضيات المتقطعة
الجبر
الضبابية
نظرية المجموعات
نظرية الزمر
نظرية الحلقات والحقول
نظرية الاعداد
نظرية الفئات
حساب المتجهات
المتتاليات-المتسلسلات
المصفوفات و نظريتها
المثلثات
الهندسة
التفاضل و التكامل
المعادلات التفاضلية و التكاملية
التحليل
التبلوجيا
نظرية الالعاب
الاحتمالات و الاحصاء
نظرية التحكم
بحوث العمليات
نظرية الكم
الشفرات
الرياضيات التطبيقية
نظريات ومبرهنات
علماء الرياضيات
الرياضيات في العلوم الاخرى
بحوث و اطاريح جامعية
هل تعلم
طرائق التدريس
الرياضيات العامة
نظرية البيان

Untitled Document
أبحث عن شيء أخر المرجع الالكتروني للمعلوماتية
أضيف حديثاً
ظهور التلسكوبات
2025-01-12
آثار فسخ عقد الزواج بعد الدخول بالنسبة للنفقة في قانون الاحوال الشخصية الكويتي
2025-01-12
نضج وحصاد وتخزين البسلة
2025-01-12
مقبرة (شيشنق الثالث)
2025-01-12
الفرعون شيشنق الرابع وآثاره
2025-01-12
مندوبات الصلاة
2025-01-12

وثائقيات
العباءة العربية .. إرث الآباء واعتزاز الأبناء
التاريخ / 20-09-2024

مختارات
الكَمَرَئي (.ت/ 1115هـ)
20-6-2016
التـراكم ، الادخـار ، والاستثمـار في الدول الناميـة
3-1-2020
Quadratic Integral
17-9-2018
Linkage
16-10-2021
الابواب والشبابيك
2023-03-22
التخطيـط للقرار الستراتيجـي والتكتيكـي
8-3-2019

Jacobi Function of the Second Kind  
  
1607   03:13 مساءً   date: 21-7-2019
Author : Szegö, G.
Book or Source : "Jacobi Polynomials." Ch. 4 in Orthogonal Polynomials, 4th ed. Providence, RI: Amer. Math. Soc.
Page and Part : pp. 73-79


Read More
Inverse Hyperbolic Cosecant
Date: 3-6-2019 2004
Power
Date: 16-8-2019 3119
Elsasser Function
Date: 31-7-2019 1912

Jacobi Function of the Second Kind

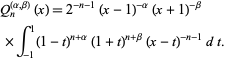Q_n^((alpha,beta))(x)=2^(-n-1)(x-1)^(-alpha)(x+1)^(-beta) ×int_(-1)^1(1-t)^(n+alpha)(1+t)^(n+beta)(x-t)^(-n-1)dt.

In the exceptional case 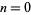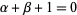n=0, alpha+beta+1=0, a nonconstant solution is given by

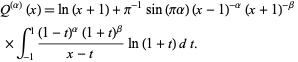Q^((alpha))(x)=ln(x+1)+pi^(-1)sin(pialpha)(x-1)^(-alpha)(x+1)^(-beta) ×int_(-1)^1((1-t)^alpha(1+t)^beta)/(x-t)ln(1+t)dt.

REFERENCES:

Szegö, G. "Jacobi Polynomials." Ch. 4 in Orthogonal Polynomials, 4th ed. Providence, RI: Amer. Math. Soc., pp. 73-79, 1975.




الجبر أحد الفروع الرئيسية في الرياضيات، حيث إن التمكن من الرياضيات يعتمد على الفهم السليم للجبر. ويستخدم المهندسون والعلماء الجبر يومياً، وتعول المشاريع التجارية والصناعية على الجبر لحل الكثير من المعضلات التي تتعرض لها. ونظراً لأهمية الجبر في الحياة العصرية فإنه يدرّس في المدارس والجامعات في جميع أنحاء العالم. ويُعجب الكثير من الدارسين للجبر بقدرته وفائدته الكبيرتين، إذ باستخدام الجبر يمكن للمرء أن يحل كثيرًا من المسائل التي يتعذر حلها باستخدام الحساب فقط.وجاء اسمه من كتاب عالم الرياضيات والفلك والرحالة محمد بن موسى الخورازمي.


يعتبر علم المثلثات Trigonometry علماً عربياً ، فرياضيو العرب فضلوا علم المثلثات عن علم الفلك كأنهما علمين متداخلين ، ونظموه تنظيماً فيه لكثير من الدقة ، وقد كان اليونان يستعملون وتر CORDE ضعف القوسي قياس الزوايا ، فاستعاض رياضيو العرب عن الوتر بالجيب SINUS فأنت هذه الاستعاضة إلى تسهيل كثير من الاعمال الرياضية.

تعتبر المعادلات التفاضلية خير وسيلة لوصف معظم المـسائل الهندسـية والرياضـية والعلمية على حد سواء، إذ يتضح ذلك جليا في وصف عمليات انتقال الحرارة، جريان الموائـع، الحركة الموجية، الدوائر الإلكترونية فضلاً عن استخدامها في مسائل الهياكل الإنشائية والوصف الرياضي للتفاعلات الكيميائية.
ففي في الرياضيات, يطلق اسم المعادلات التفاضلية على المعادلات التي تحوي مشتقات و تفاضلات لبعض الدوال الرياضية و تظهر فيها بشكل متغيرات المعادلة . و يكون الهدف من حل هذه المعادلات هو إيجاد هذه الدوال الرياضية التي تحقق مشتقات هذه المعادلات.





الأخبار الصحية
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
التاريخ / 2025-01-09

الأخبار العلمية
القمر "يبتلع" المريخ!
التاريخ / 2025-01-09

الساحة الاسلامية
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
التاريخ / 2025-01-12