


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 15-6-2019
Date: 12-10-2018
Date: 3-9-2019
|
There are a great many beautiful identities involving 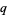 -series, some of which follow directly by taking the q-analog of standard combinatorial identities, e.g., the q-binomial theorem
-series, some of which follow directly by taking the q-analog of standard combinatorial identities, e.g., the q-binomial theorem
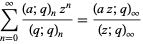 |
(1) |
(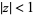 ,
, 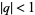 ; Andrews 1986, p. 10), a special case of an identity due to Euler
; Andrews 1986, p. 10), a special case of an identity due to Euler
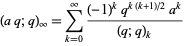 |
(2) |
(Gasper and Rahman 1990, p. 9; Leininger and Milne 1999), and q-Vandermonde sum
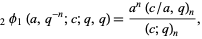 |
(3) |
where 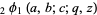 is a q-hypergeometric function.
is a q-hypergeometric function.
Other 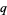 -series identities, e.g., the Jacobi identities, Rogers-Ramanujan identities, and q-hypergeometric identity
-series identities, e.g., the Jacobi identities, Rogers-Ramanujan identities, and q-hypergeometric identity
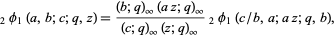 |
(4) |
seem to arise out of the blue. Another such example is
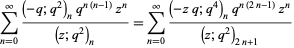 |
(5) |
(Gordon and McIntosh 2000).
Hirschhorn (1999) gives the beautiful identity
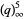 |
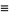 |
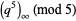 |
(6) |
 |
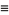 |
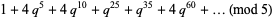 |
(7) |
(OEIS A098445). Other modular identities involving the q-series 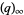 include
include
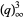 |
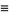 |
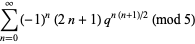 |
(8) |
 |
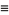 |
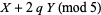 |
(9) |
(Hardy and Wright 1979, Hirschhorn 1999), where
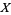 |
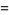 |
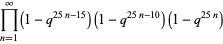 |
(10) |
 |
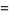 |
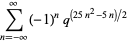 |
(11) |
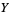 |
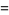 |
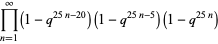 |
(12) |
 |
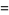 |
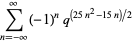 |
(13) |
(Hirschhorn 1999).
Zucker (1990) defines the useful notations
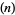 |
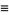 |
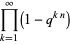 |
(14) |
 |
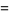 |
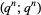 |
(15) |
![[n]](http://mathworld.wolfram.com/images/equations/q-SeriesIdentities/Inline37.gif) |
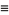 |
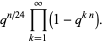 |
(16) |
A set of beautiful identities that can be expressed in this notation were found by M. Trott (pers. comm., Dec. 19, 2000),
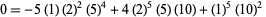 |
(17) |
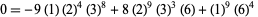 |
(18) |
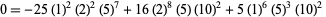 |
(19) |
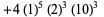 |
(20) |
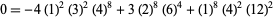 |
(21) |
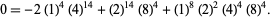 |
(22) |
These are closely related to modular equation identities. For example, equation (◇) is an elegant form of Shen (1994) equation (3.12), obtained using the identities
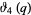 |
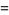 |
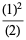 |
(23) |
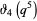 |
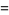 |
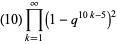 |
(24) |
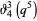 |
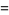 |
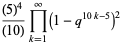 |
(25) |
(OEIS A002448, A089803, and A089804). Similarly, equation (◇) is actually the classical expression
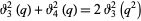 |
(26) |
for the Jacobi theta functions which follows from
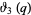 |
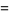 |
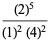 |
(27) |
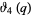 |
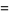 |
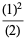 |
(28) |
(J. Zucker, pers. comm., Nov. 11, 2003).
Another set of identities found by M. Trott (pers. comm., Jul. 8, 2009) are given by
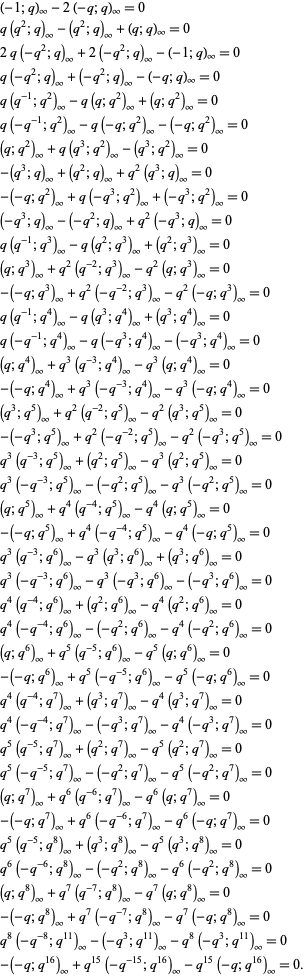 |
(29) |
REFERENCES:
Andrews, G. E. q-Series: Their Development and Application in Analysis, Number Theory, Combinatorics, Physics, and Computer Algebra. Providence, RI: Amer. Math. Soc., 1986.
Berndt, B. C. "Modular Equations of Degrees 3, 5, and 7 and Associated Theta-Function Identities." Ch. 19 in Ramanujan's Notebooks, Part III. New York:Springer-Verlag, pp. 220-324, 1985.
Gasper, G. and Rahman, M. Basic Hypergeometric Series. Cambridge, England: Cambridge University Press, 1990.
Gordon, B. and McIntosh, R. J. "Some Eighth Order Mock Theta Functions." J. London Math. Soc. 62, 321-335, 2000.
Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, 1979.
Hirschhorn, M. D. "Another Short Proof of Ramanujan's Mod 5 Partition Congruences, and More." Amer. Math. Monthly 106, 580-583, 1999.
Leininger, V. E. and Milne, S. C. "Some New Infinite Families of 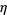 -Function Identities." Methods Appl. Anal. 6, 225-248, 1999.
-Function Identities." Methods Appl. Anal. 6, 225-248, 1999.
Shen, L.-C. "On the Additive Formulae of the Theta Functions and a Collection of Lambert Series Pertaining to the Modular Equations of Degree 5." Trans. Amer. Math. Soc. 345, 323-345, 1994.
Sloane, N. J. A. Sequences A002448, A089803, A089804, and A098445 in "The On-Line Encyclopedia of Integer Sequences."
Zucker, J. "Further Relations Amongst Infinite Series and Products. II. The Evaluation of Three-Dimensional Lattice Sums." J. Phys. A: Math. Gen. 23, 117-132, 1990.



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
في مدينة الهرمل اللبنانية.. وفد العتبة الحسينية المقدسة يستمر بإغاثة العوائل السورية المنكوبة
|
|
|