


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 19-2-2020
Date: 22-7-2020
Date: 13-9-2020
|
What is the sofa of greatest area 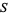 which can be moved around a right-angled hallway of unit width? Hammersley (Croft et al. 1994) showed that
which can be moved around a right-angled hallway of unit width? Hammersley (Croft et al. 1994) showed that
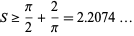 |
(1) |
(OEIS A086118). Gerver (1992) found a sofa with larger area and provided arguments indicating that it is either optimal or close to it. The boundary of Gerver's sofa is a complicated shape composed of 18 arcs. Its area can be given by defining the constants 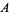 ,
, 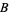 ,
, 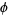 , and
, and 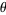 by solving
by solving
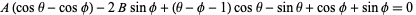 |
(2) |
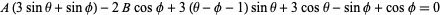 |
(3) |
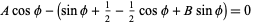 |
(4) |
![(A+1/2pi-phi-theta)-[B-1/2(theta-phi)(1+A)-1/4(theta-phi)^2]=0.](http://mathworld.wolfram.com/images/equations/MovingSofaProblem/Inline9.gif) |
(5) |
This gives
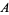 |
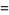 |
 |
(6) |
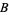 |
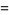 |
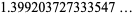 |
(7) |
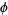 |
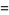 |
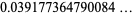 |
(8) |
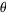 |
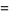 |
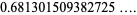 |
(9) |
Now define
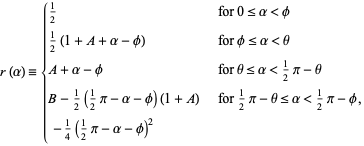 |
(10) |
where
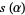 |
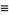 |
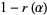 |
(11) |
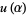 |
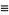 |
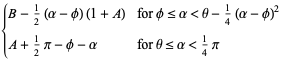 |
(12) |
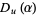 |
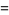 |
 |
(13) |
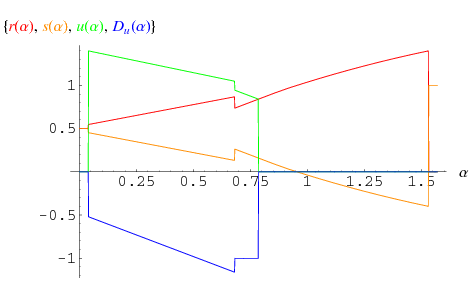
Finally, define the functions
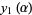 |
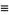 |
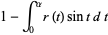 |
(14) |
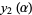 |
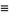 |
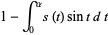 |
(15) |
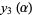 |
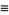 |
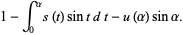 |
(16) |
The area of the optimal sofa is then given by
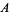 |
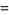 |
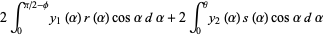 |
![+2int_phi^(pi/4)y_3(alpha)[u(alpha)sinalpha-D_u(alpha)cosalpha-s(alpha)cosalpha]dalpha](http://mathworld.wolfram.com/images/equations/MovingSofaProblem/Inline43.gif) |
(17) |
 |
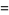 |
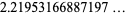 |
(18) |
(Finch 2003).
REFERENCES:
Croft, H. T.; Falconer, K. J.; and Guy, R. K. Unsolved Problems in Geometry. New York: Springer-Verlag, 1994.
Finch, S. R. "Moving Sofa Constant." §8.12 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 519-523, 2003.
Gerver, J. L. "On Moving a Sofa Around a Corner." Geometriae Dedicata 42, 267-283, 1992.
Sloane, N. J. A. Sequence A086118 in "The On-Line Encyclopedia of Integer Sequences."
Stewart, I. Another Fine Math You've Got Me Into.... New York: W. H. Freeman, 1992.
Trott, M. The Mathematica GuideBook for Programming. New York: Springer-Verlag, p. 104, 2004. http://www.mathematicaguidebooks.org/.



|
|
|
|
دراسة تكشف "مفاجأة" غير سارة تتعلق ببدائل السكر
|
|
|
|
|
|
|
أدوات لا تتركها أبدًا في سيارتك خلال الصيف!
|
|
|
|
|
|
|
العتبة العباسية المقدسة تؤكد الحاجة لفنّ الخطابة في مواجهة تأثيرات الخطابات الإعلامية المعاصرة
|
|
|