


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 20-11-2019
Date: 22-12-2020
Date: 10-10-2020
|
Let 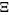 be the xi-function defined by
be the xi-function defined by
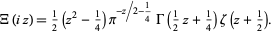 |
(1) |
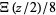 can be viewed as the Fourier transform of the signal
can be viewed as the Fourier transform of the signal
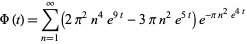 |
(2) |
for 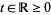 . Then denote the Fourier transform of
. Then denote the Fourier transform of 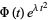 as
as 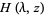 ,
,
=H(lambda,z).](http://mathworld.wolfram.com/images/equations/deBruijn-NewmanConstant/NumberedEquation3.gif) |
(3) |
de Bruijn (1950) proved that 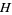 has only real zeros for
has only real zeros for 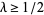 . C. M. Newman (1976) proved that there exists a constant
. C. M. Newman (1976) proved that there exists a constant 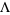 such that
such that 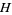 has only real zeros iff
has only real zeros iff 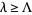 . The best current lower bound (Csordas et al. 1993, 1994) is
. The best current lower bound (Csordas et al. 1993, 1994) is 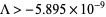 . The Riemann hypothesis is equivalent to the conjecture that
. The Riemann hypothesis is equivalent to the conjecture that 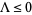 .
.
REFERENCES:
Csordas, G.; Odlyzko, A.; Smith, W.; and Varga, R. S. "A New Lehmer Pair of Zeros and a New Lower Bound for the de Bruijn-Newman Constant." Elec. Trans. Numer. Analysis 1, 104-111, 1993.
Csordas, G.; Smith, W.; and Varga, R. S. "Lehmer Pairs of Zeros, the de Bruijn-Newman Constant and the Riemann Hypothesis." Constr. Approx. 10, 107-129, 1994.
de Bruijn, N. G. "The Roots of Trigonometric Integrals." Duke Math. J. 17, 197-226, 1950.
Finch, S. R. "De Bruijn-Newman Constant." §2.3 2 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 203-205, 2003.
Newman, C. M. "Fourier Transforms with only Real Zeros." Proc. Amer. Math. Soc. 61, 245-251, 1976.



|
|
|
|
دراسة تكشف "مفاجأة" غير سارة تتعلق ببدائل السكر
|
|
|
|
|
|
|
أدوات لا تتركها أبدًا في سيارتك خلال الصيف!
|
|
|
|
|
|
|
العتبة العباسية المقدسة تؤكد الحاجة لفنّ الخطابة في مواجهة تأثيرات الخطابات الإعلامية المعاصرة
|
|
|