


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 21-11-2019
Date: 6-4-2020
Date: 31-8-2020
|
The 8.1.2 equation
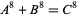 |
(1) |
is a special case of Fermat's last theorem with 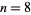 , and so has no solution. No 8.1.3, 8.1.4, 8.1.5, 8.1.6, or 8.1.7 solutions are known. The only known 8.1.8 is
, and so has no solution. No 8.1.3, 8.1.4, 8.1.5, 8.1.6, or 8.1.7 solutions are known. The only known 8.1.8 is
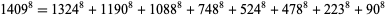 |
(2) |
(S. Chase; Meyrignac). The smallest 8.1.9 is
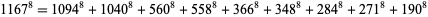 |
(3) |
(N. Kuosa). The smallest 8.1.10 is
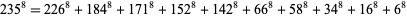 |
(4) |
(N. Kuosa, PowerSum). The smallest 8.1.11 solution is
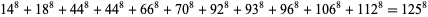 |
(5) |
(Lander et al. 1967, Ekl 1998). The smallest 8.1.12 solution is
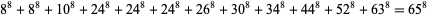 |
(6) |
(Lander et al. 1967). The general identity
![(2^(8k+4)+1)^8=(2^(8k+4)-1)^8+(2^(7k+4))^8+(2^(k+1))^8+7[(2^(5k+3))^8+(2^(3k+2))^8]](https://mathworld.wolfram.com/images/equations/DiophantineEquation8thPowers/NumberedEquation7.gif) |
(7) |
gives a solution to the 8.1.17 equation (Lander et al. 1967).
No 8.2.2, 8.2.3, 8.2.4, 8.2.5, or 8.2.6 solution is known. A single 8.2.7 solutions is known,
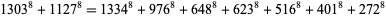 |
(8) |
(S. Chase; Meyrignac). The smallest 8.2.8 solution is
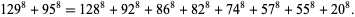 |
(9) |
The smallest 8.2.9 solution is
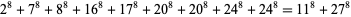 |
(10) |
(Lander et al. 1967, Ekl 1998).
No 8.3.3 or 8.3.4 solutions are known. An 8.3.5 solution is
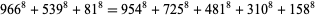 |
(11) |
(S. Chase, Meyrignac, Resta and Meyrignac 2003). No 8.3.6 solution is known. The smallest 8.3.7 solution is
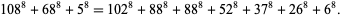 |
(12) |
The smallest 8.3.8 solution is
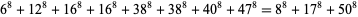 |
(13) |
(Lander et al. 1967, Ekl 1998).
The 8.4.4 solution
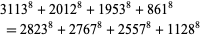 |
(14) |
was found by Nuutti Kuosa.
The smallest 8.4.5 solution is
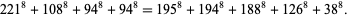 |
(15) |
The smallest 8.4.6 solution is
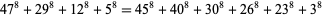 |
(16) |
(Ekl 1998). The smallest 8.4.7 solution is
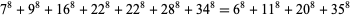 |
(17) |
(Lander et al. 1967).
The smallest 8.5.5 solutions are
 |
(18) |
(Letac 1942, Lander et al. 1967, Ekl 1998). The smallest 8.5.6 solutions are
 |
(19) |
(Ekl 1998).
Moessner and Gloden (1944) found solutions to the 8.6.6 equation. The smallest 8.6.6 solution is
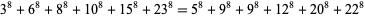 |
(20) |
(Lander et al. 1967). Ekl (1998) mentions but does not list 204 primitive solutions to the 8.6.6 equation. Moessner and Gloden (1944) found solutions to the 8.6.7 equation.
Parametric solutions to the 8.7.7 equation were given by Moessner (1947) and Gloden (1948). The smallest 8.7.7 solution is
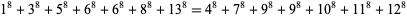 |
(21) |
(Lander et al. 1967).
Sastry (1934) used the smallest 17-1 solution to give a parametric 8.8.8 solution. The smallest 8.8.8 solution is
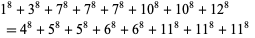 |
(22) |
(Lander et al. 1967).
Letac (1942) found solutions to the 8.9.9 equation.
Moessner and Gloden (1944) found the 8.9.10 solution
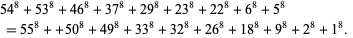 |
(23) |
REFERENCES:
Ekl, R. L. "New Results in Equal Sums of Like Powers." Math. Comput. 67, 1309-1315, 1998.
Gloden, A. "Parametric Solutions of Two Multi-Degreed Equalities." Amer. Math. Monthly 55, 86-88, 1948.
Lander, L. J.; Parkin, T. R.; and Selfridge, J. L. "A Survey of Equal Sums of Like Powers." Math. Comput. 21, 446-459, 1967.
Letac, A. Gazetta Mathematica 48, 68-69, 1942.
Meyrignac, J.-C. "Computing Minimal Equal Sums of Like Powers." https://euler.free.fr.
Moessner, A. "On Equal Sums of Like Powers." Math. Student 15, 83-88, 1947.
Moessner, A. and Gloden, A. "Einige Zahlentheoretische Untersuchungen und Resultate." Bull. Sci. École Polytech. de Timisoara 11, 196-219, 1944.
Resta, G. and Meyrignac, J.-C. "The Smallest Solutions to the Diophantine Equation 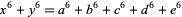 ." Math. Comput. 72, 1051-1054, 2003.
." Math. Comput. 72, 1051-1054, 2003.
Sastry, S. "On Sums of Powers." J. London Math. Soc. 9, 242-246, 1934.



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
في مدينة الهرمل اللبنانية.. وفد العتبة الحسينية المقدسة يستمر بإغاثة العوائل السورية المنكوبة
|
|
|