


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 4-2-2020
Date: 13-1-2021
Date: 21-12-2020
|
A special case of the quadratic Diophantine equation having the form
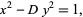 |
(1) |
where 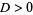 is a nonsquare natural number (Dickson 2005). The equation
is a nonsquare natural number (Dickson 2005). The equation
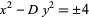 |
(2) |
arising in the computation of fundamental units is sometimes also called the Pell equation (Dörrie 1965, Itô 1987), and Dörrie calls the positive form of (2) the Fermat difference equation. While Fermat deserves credit for being the first to extensively study the equation, the erroneous attribution to Pell was perpetrated by none other than Euler himself (Nagell 1951, p. 197; Burton 1989; Dickson 2005, p. 341). The Pell equation was also solved by the Indian mathematician Bhaskara. Pell equations are extremely important in number theory, and arise in the investigation of numbers which are figurate in more than one way, for example, simultaneously square and triangular.
The equation has an obvious generalization to the Pell-like equation
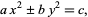 |
(3) |
as well as the general second-order bivariate Diophantine equation
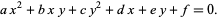 |
(4) |
However, several different techniques are required to solve this equation for arbitrary values of 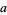 ,
, 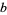 , and
, and 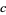 . The Wolfram Language command Reduce[f[x, y] && Element[x|y, Integers]] finds solutions to the general equation (4) when they exist.
. The Wolfram Language command Reduce[f[x, y] && Element[x|y, Integers]] finds solutions to the general equation (4) when they exist.
Pell equations of the form (1), as well as certain cases of the analogous equation with a minus sign on the right,
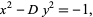 |
(5) |
can be solved by finding the continued fraction ![[a_0,a_1,...]](https://mathworld.wolfram.com/images/equations/PellEquation/Inline5.gif) of
of 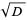 . Note that although the equation (5) is solvable for only certain values of
. Note that although the equation (5) is solvable for only certain values of  , the continued fraction technique provides solutions when they exist, and always in the case of (1), for which a solution always exists. A necessary condition that (5) be solvable is that all odd prime factors of
, the continued fraction technique provides solutions when they exist, and always in the case of (1), for which a solution always exists. A necessary condition that (5) be solvable is that all odd prime factors of  be of the form
be of the form 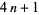 , and that
, and that 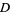 cannot be doubly even (i.e., divisible by 4). However, these conditions are not sufficient for a solution to exist, as demonstrated by the equation
cannot be doubly even (i.e., divisible by 4). However, these conditions are not sufficient for a solution to exist, as demonstrated by the equation 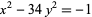 , which has no solutions in integers (Nagell 1951, pp. 201 and 204).
, which has no solutions in integers (Nagell 1951, pp. 201 and 204).
In all subsequent discussion, ignore the trivial solution 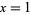 ,
, 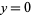 . Let
. Let 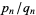 denote the
denote the 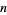 th convergent
th convergent ![[a_0,a_1,...,a_n]](https://mathworld.wolfram.com/images/equations/PellEquation/Inline16.gif) , then we will have solved (1) or (5) if we can find a convergent which obeys the identity
, then we will have solved (1) or (5) if we can find a convergent which obeys the identity
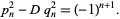 |
(6) |
Amazingly, this turns out to always be possible as a result of the fact that the continued fraction of a quadratic surd always becomes periodic at some term 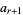 , where
, where 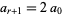 , i.e.,
, i.e.,
![sqrt(D)=[a_0,a_1,...,a_r,2a_0^_].](https://mathworld.wolfram.com/images/equations/PellEquation/NumberedEquation7.gif) |
(7) |
To compute the continued fraction convergents to 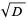 , use the usual recurrence relations
, use the usual recurrence relations
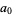 |
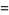 |
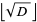 |
(8) |
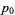 |
 |
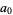 |
(9) |
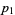 |
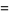 |
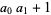 |
(10) |
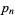 |
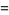 |
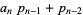 |
(11) |
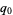 |
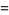 |
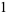 |
(12) |
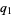 |
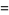 |
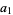 |
(13) |
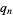 |
 |
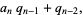 |
(14) |
where 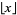 is the floor function. For reasons to be explained shortly, also compute the two additional quantities
is the floor function. For reasons to be explained shortly, also compute the two additional quantities 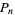 and
and 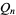 defined by
defined by
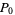 |
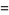 |
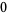 |
(15) |
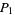 |
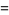 |
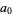 |
(16) |
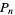 |
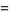 |
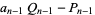 |
(17) |
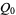 |
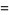 |
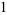 |
(18) |
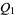 |
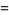 |
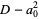 |
(19) |
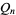 |
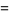 |
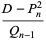 |
(20) |
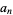 |
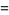 |
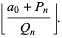 |
(21) |
Now, two important identities satisfied by continued fraction convergents are
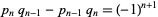 |
(22) |
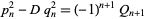 |
(23) |
(Beiler 1966, p. 262), so both linear
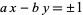 |
(24) |
and quadratic
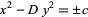 |
(25) |
equations are solved simply by finding an appropriate continued fraction.
Let 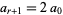 be the term at which the continued fraction becomes periodic (which will always happen for a quadratic surd). For the Pell equation
be the term at which the continued fraction becomes periodic (which will always happen for a quadratic surd). For the Pell equation
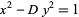 |
(26) |
with 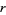 odd,
odd, 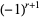 is positive and the solution in terms of smallest integers is
is positive and the solution in terms of smallest integers is 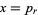 and
and 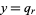 , where
, where 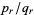 is the
is the 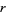 th convergent. If
th convergent. If 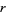 is even, then
is even, then 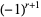 is negative, but
is negative, but
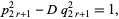 |
(27) |
so the solution in smallest integers is 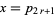 ,
, 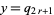 . Summarizing,
. Summarizing,
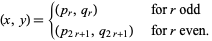 |
(28) |
The equation
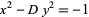 |
(29) |
can be solved analogously to the equation with 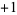 on the right side iff
on the right side iff 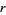 is even, but has no solution if
is even, but has no solution if 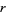 is odd,
is odd,
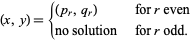 |
(30) |
Given one solution 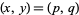 (which can be found as above), a whole family of solutions can be found by taking each side to the
(which can be found as above), a whole family of solutions can be found by taking each side to the 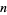 th power,
th power,
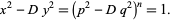 |
(31) |
Factoring gives
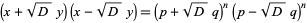 |
(32) |
and
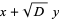 |
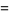 |
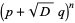 |
(33) |
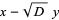 |
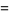 |
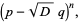 |
(34) |
which gives the family of solutions
 |
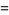 |
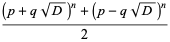 |
(35) |
 |
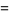 |
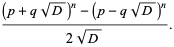 |
(36) |
These solutions also hold for
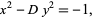 |
(37) |
except that 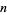 can take on only odd values.
can take on only odd values.
The following table gives the smallest integer solutions 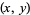 to the Pell equation with constant
to the Pell equation with constant 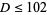 (Beiler 1966, p. 254). Square
(Beiler 1966, p. 254). Square 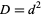 are not included, since they would result in an equation of the form
are not included, since they would result in an equation of the form
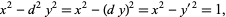 |
(38) |
which has no solutions (since the difference of two squares cannot be 1).
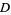 |
 |
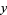 |
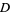 |
 |
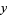 |
| 2 | 3 | 2 | 54 | 485 | 66 |
| 3 | 2 | 1 | 55 | 89 | 12 |
| 5 | 9 | 4 | 56 | 15 | 2 |
| 6 | 5 | 2 | 57 | 151 | 20 |
| 7 | 8 | 3 | 58 | 19603 | 2574 |
| 8 | 3 | 1 | 59 | 530 | 69 |
| 10 | 19 | 6 | 60 | 31 | 4 |
| 11 | 10 | 3 | 61 | 1766319049 | 226153980 |
| 12 | 7 | 2 | 62 | 63 | 8 |
| 13 | 649 | 180 | 63 | 8 | 1 |
| 14 | 15 | 4 | 65 | 129 | 16 |
| 15 | 4 | 1 | 66 | 65 | 8 |
| 17 | 33 | 8 | 67 | 48842 | 5967 |
| 18 | 17 | 4 | 68 | 33 | 4 |
| 19 | 170 | 39 | 69 | 7775 | 936 |
| 20 | 9 | 2 | 70 | 251 | 30 |
| 21 | 55 | 12 | 71 | 3480 | 413 |
| 22 | 197 | 42 | 72 | 17 | 2 |
| 23 | 24 | 5 | 73 | 2281249 | 267000 |
| 24 | 5 | 1 | 74 | 3699 | 430 |
| 26 | 51 | 10 | 75 | 26 | 3 |
| 27 | 26 | 5 | 76 | 57799 | 6630 |
| 28 | 127 | 24 | 77 | 351 | 40 |
| 29 | 9801 | 1820 | 78 | 53 | 6 |
| 30 | 11 | 2 | 79 | 80 | 9 |
| 31 | 1520 | 273 | 80 | 9 | 1 |
| 32 | 17 | 3 | 82 | 163 | 18 |
| 33 | 23 | 4 | 83 | 82 | 9 |
| 34 | 35 | 6 | 84 | 55 | 6 |
| 35 | 6 | 1 | 85 | 285769 | 30996 |
| 37 | 73 | 12 | 86 | 10405 | 1122 |
| 38 | 37 | 6 | 87 | 28 | 3 |
| 39 | 25 | 4 | 88 | 197 | 21 |
| 40 | 19 | 3 | 89 | 500001 | 53000 |
| 41 | 2049 | 320 | 90 | 19 | 2 |
| 42 | 13 | 2 | 91 | 1574 | 165 |
| 43 | 3482 | 531 | 92 | 1151 | 120 |
| 44 | 199 | 30 | 93 | 12151 | 1260 |
| 45 | 161 | 24 | 94 | 2143295 | 221064 |
| 46 | 24335 | 3588 | 95 | 39 | 4 |
| 47 | 48 | 7 | 96 | 49 | 5 |
| 48 | 7 | 1 | 97 | 62809633 | 6377352 |
| 50 | 99 | 14 | 98 | 99 | 10 |
| 51 | 50 | 7 | 99 | 10 | 1 |
| 52 | 649 | 90 | 101 | 201 | 20 |
| 53 | 66249 | 9100 | 102 | 101 | 10 |
The first few minimal values of  and
and 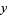 for nonsquare
for nonsquare 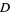 are 3, 2, 9, 5, 8, 3, 19, 10, 7, 649, ... (OEIS A033313) and 2, 1, 4, 2, 3, 1, 6, 3, 2, 180, ... (OEIS A033317), respectively. The values of
are 3, 2, 9, 5, 8, 3, 19, 10, 7, 649, ... (OEIS A033313) and 2, 1, 4, 2, 3, 1, 6, 3, 2, 180, ... (OEIS A033317), respectively. The values of 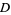 having
having 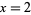 , 3, ... are 3, 2, 15, 6, 35, 12, 7, 5, 11, 30, ... (OEIS A033314) and the values of
, 3, ... are 3, 2, 15, 6, 35, 12, 7, 5, 11, 30, ... (OEIS A033314) and the values of 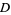 having
having 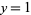 , 2, ... are 3, 2, 7, 5, 23, 10, 47, 17, 79, 26, ... (OEIS A033318). Values of the incrementally largest minimal
, 2, ... are 3, 2, 7, 5, 23, 10, 47, 17, 79, 26, ... (OEIS A033318). Values of the incrementally largest minimal  are 3, 9, 19, 649, 9801, 24335, 66249, ... (OEIS A033315) which occur at
are 3, 9, 19, 649, 9801, 24335, 66249, ... (OEIS A033315) which occur at 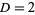 , 5, 10, 13, 29, 46, 53, 61, 109, 181, ... (OEIS A033316). Values of the incrementally largest minimal
, 5, 10, 13, 29, 46, 53, 61, 109, 181, ... (OEIS A033316). Values of the incrementally largest minimal 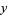 are 2, 4, 6, 180, 1820, 3588, 9100, 226153980, ... (OEIS A033319), which occur at
are 2, 4, 6, 180, 1820, 3588, 9100, 226153980, ... (OEIS A033319), which occur at 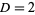 , 5, 10, 13, 29, 46, 53, 61, ... (OEIS A033316).
, 5, 10, 13, 29, 46, 53, 61, ... (OEIS A033316).
The more complicated Pell-like equation
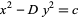 |
(39) |
with 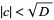 has solution iff
has solution iff 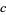 is one of the values
is one of the values 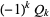 for
for 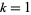 , 2, ...,
, 2, ..., 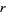 computed in the process of finding the convergents to
computed in the process of finding the convergents to 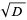 (where, as above,
(where, as above, 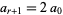 is the term at which the continued fraction becomes periodic). If
is the term at which the continued fraction becomes periodic). If 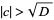 , the procedure is significantly more complicated (Beiler 1966, p. 265; Dickson 2005, pp. 387-388) and is discussed by Gérardin (1910) and Chrystal (1961).
, the procedure is significantly more complicated (Beiler 1966, p. 265; Dickson 2005, pp. 387-388) and is discussed by Gérardin (1910) and Chrystal (1961).
Regardless of how it is found, if a single solution 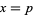 ,
, 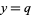 to (39) is known, other solutions can be found. Let
to (39) is known, other solutions can be found. Let 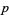 and
and 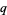 be solutions to (39), and
be solutions to (39), and 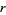 and
and 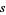 solutions to the "unit" form
solutions to the "unit" form
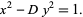 |
(40) |
Then the identity
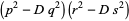 |
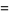 |
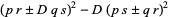 |
(41) |
 |
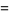 |
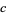 |
(42) |
allows larger solutions 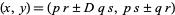 to the
to the 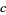 equation to be found by using incrementally larger values of the
equation to be found by using incrementally larger values of the 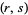 , which can be easily computed using the standard technique for the Pell equation. Such a family of solutions does not necessarily generate all solutions, however. For example, the equation
, which can be easily computed using the standard technique for the Pell equation. Such a family of solutions does not necessarily generate all solutions, however. For example, the equation
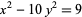 |
(43) |
has three distinct sets of fundamental solutions, 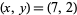 , (13, 4), and (57, 18). Using (42), these generate the solutions shown in the following table, from which the set of all solutions (7, 2), (13, 4), (57, 18), (253, 80), (487, 154), (2163, 684), (9607, 3038), ... can be generated.
, (13, 4), and (57, 18). Using (42), these generate the solutions shown in the following table, from which the set of all solutions (7, 2), (13, 4), (57, 18), (253, 80), (487, 154), (2163, 684), (9607, 3038), ... can be generated.
| fundamental | generated solutions |
| (7, 2) | (253, 80), (9607, 3038), (364813, 115364), (13853287, 4380794), ... |
| (13, 4) | (487, 154), (18493, 5848), (702247, 222070), (26666893, 8432812), ... |
| (57, 18) | (2163, 684), (82137, 25974), (3119043, 986328), (118441497, 37454490), ... |
The case
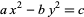 |
(44) |
can be reduced to the one above by multiplying through by 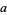 ,
,
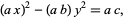 |
(45) |
finding solutions in 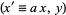 , and then selecting those for which
, and then selecting those for which 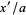 is an integer.
is an integer.
According to Dickson (2005, pp. 408 and 411), the equation
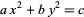 |
(46) |
with 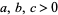 , which has either no solutions or a finite number of solutions, was solved by Gauss in 1863 using the method of exclusions and considered by Euler (1773) and Nasimoff (1885), although Euler's methods were incomplete (Smith 1965; Dickson 2005, p. 378). According to Itô (1987), this equation can be solved completely using solutions to Pell's equation. Nasimoff (1885) applied Jacobi elliptic functions to express the number of solutions of this equation for
, which has either no solutions or a finite number of solutions, was solved by Gauss in 1863 using the method of exclusions and considered by Euler (1773) and Nasimoff (1885), although Euler's methods were incomplete (Smith 1965; Dickson 2005, p. 378). According to Itô (1987), this equation can be solved completely using solutions to Pell's equation. Nasimoff (1885) applied Jacobi elliptic functions to express the number of solutions of this equation for 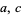 odd (Dickson 2005, p. 411). Additional discussion including the connection with elliptic functions is given in Dickson (2005, pp. 387-391).
odd (Dickson 2005, p. 411). Additional discussion including the connection with elliptic functions is given in Dickson (2005, pp. 387-391).
The special case of 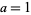 and
and 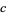 prime was solved by Cornacchia (Cornacchia 1908, Cox 1989, Wagon 1990). A deterministic algorithm for finding all primitive solutions to (46) for
prime was solved by Cornacchia (Cornacchia 1908, Cox 1989, Wagon 1990). A deterministic algorithm for finding all primitive solutions to (46) for 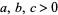 fixed relatively prime integers,
fixed relatively prime integers, 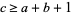 , and
, and 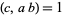 was given by Hardy et al. (1990). This algorithm generalizes those of Hermite (1848), Serret (1848), Brillhart (1972), Cornacchia (1908), and Wilker (1980). It requires factorization of
was given by Hardy et al. (1990). This algorithm generalizes those of Hermite (1848), Serret (1848), Brillhart (1972), Cornacchia (1908), and Wilker (1980). It requires factorization of 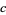 , and has worst case running time of
, and has worst case running time of 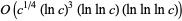 , independent of
, independent of 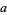 and
and 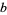 . An algorithmic method for finding all solutions is implemented in the Wolfram Language as Reduce[x^2 + d y^2 == n,
. An algorithmic method for finding all solutions is implemented in the Wolfram Language as Reduce[x^2 + d y^2 == n, 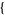 x, y
x, y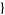 , Integers].
, Integers].
REFERENCES:
Beiler, A. H. "The Pellian." Ch. 22 in Recreations in the Theory of Numbers: The Queen of Mathematics Entertains. New York: Dover, pp. 248-268, 1966.
Brillhart, J. "Note on Representing a Prime as a Sum of Two Squares." Math. Comput. 26, 1011-1013, 1972.
Burton, D. M. Elementary Number Theory, 4th ed. Boston, MA: Allyn and Bacon, pp. 379-382 and 392, 1989.
Chrystal, G. Textbook of Algebra, 2nd ed., Vol. 2. New York: Chelsea, pp. 478-486, 1961.
Cipolla, M. "Un metodo per la risoluzione della congruenza di secondo grado." Rend. Accad. Sci. Fis. Mat. Napoli 9, 154-163, 1903.
Cohn, H. "Pell's Equation." §6.9 in Advanced Number Theory. New York: Dover, pp. 110-111, 1980.
Cornacchia, G. "Su di un metodo per la risoluzione in numeri unteri dell' equazione 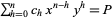 ." Giornale di Matematiche di Battaglini 46, 33-90, 1908.
." Giornale di Matematiche di Battaglini 46, 33-90, 1908.
Cox, D. A. Primes of the form 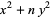 . New York: Wiley, 1989.
. New York: Wiley, 1989.
Degan, C. F. Canon Pellianus. Copenhagen, Denmark, 1817.
Dickson, L. E. "Pell Equation: 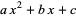 Made Square." Ch. 12 in History of the Theory of Numbers, Vol. 2: Diophantine Analysis. New York: Dover, pp. 341-400, 2005.
Made Square." Ch. 12 in History of the Theory of Numbers, Vol. 2: Diophantine Analysis. New York: Dover, pp. 341-400, 2005.
Dörrie, H. 100 Great Problems of Elementary Mathematics: Their History and Solutions. New York: Dover, 1965.
Euler, L. Novi Comm. Acad. Petrop. 18, 218, 1773. Reprinted in Opera Omnia, Series Prima, Vol. 3, p. 310.
Euler, L. Comm. Arith. 570. Reprinted in Opera Omnia, Series Prima, Vol. 3, p. 310.
Gérardin, A. "Formules de récurrence." Sphinx-Oedipe 5, 17-29, 1910.
Hardy, K.; Muskat, J. B.; and Williams, K. S. "A Deterministic Algorithm for Solving 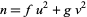 in Coprime Integers
in Coprime Integers 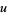 and
and 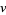 ." Math. Comput. 55, 327-343, 1990.
." Math. Comput. 55, 327-343, 1990.
Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, pp. 91-92, 2003.
Hermite, C. "Note au sujet de l'article précédent." J. Math. Pures Appl. 13, 15, 1848.
Itô, K. (Ed.). Encyclopedic Dictionary of Mathematics, 2nd ed., Vol. 1. Cambridge, MA: MIT Press, p. 450, 1987.
Lagarias, J. C. "On the Computational Complexity of Determining the Solvability or Unsolvability of the Equation 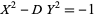 ." Trans. Amer. Math. Soc. 260, 485-508, 1980.
." Trans. Amer. Math. Soc. 260, 485-508, 1980.
Lenstra, H. W. Jr. "Solving the Pell Equation." Not. Amer. Math. Soc. 49, 182-192, 2002.
Nagell, T. "The Diophantine Equation 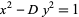 ," "The Diophantine Equation
," "The Diophantine Equation 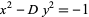 ," and "The Diophantine Equation
," and "The Diophantine Equation 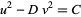 ." §56-58 in Introduction to Number Theory. New York: Wiley, pp. 195-212, 1951.
." §56-58 in Introduction to Number Theory. New York: Wiley, pp. 195-212, 1951.
Nasimoff, P. S. Ch. 1 in Application of Elliptic Functions to the Theory of Numbers. Moscow, 1885. French summary in Ann. sci. de l'École normale supér. 5, 23-31, 1888.
Robertson, J. "Home Page for John Robertson." https://www.jpr2718.org/.
Serret, J. A. "Sur un théorème rélatif aux nombres enti'eres." J. Math. Pures Appl. 13, 12-14, 1848.
Sloane, N. J. A. Sequences A033313, A033314, A033315, A033316, A033317, A033318, and A033319 in "The On-Line Encyclopedia of Integer Sequences."
Smith, H. J. S. Collected Mathematical Papers I. New York: Chelsea, pp. 195-202, 1965.
Smarandache, F. "Un metodo de resolucion de la ecuacion diofantica." Gaz. Math. 1, 151-157, 1988.
Smarandache, F. "Method to Solve the Diophantine Equation 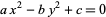 ." In Collected Papers, Vol. 1. Lupton, AZ: Erhus University Press, 1996.
." In Collected Papers, Vol. 1. Lupton, AZ: Erhus University Press, 1996.
Stillwell, J. C. Mathematics and Its History. New York: Springer-Verlag, 1989.
Wagon, S. "The Euclidean Algorithm Strikes Again." Amer. Math. Monthly 97, 124-125, 1990.
Whitford, E. E. Pell Equation. New York: Columbia University Press, 1912.
Wilker, P. "An efficient Algorithmic Solution of the Diophantine Equation 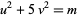 ." Math. Comput. 35, 1347-1352, 1980.
." Math. Comput. 35, 1347-1352, 1980.



|
|
|
|
دراسة تكشف "مفاجأة" غير سارة تتعلق ببدائل السكر
|
|
|
|
|
|
|
أدوات لا تتركها أبدًا في سيارتك خلال الصيف!
|
|
|
|
|
|
|
العتبة العباسية المقدسة تؤكد الحاجة لفنّ الخطابة في مواجهة تأثيرات الخطابات الإعلامية المعاصرة
|
|
|