المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Bézout Numbers |
 727
 11:28 صباحاً
date: 11-6-2020 |
Author : المرجع الالكتروني للمعلوماتيه 
Book or Source : www.almerja.com 
Page and Part : ...|
Read More
Date: 1-12-2020
673
Date: 1-12-2020
789
Date: 16-10-2019
720
|
Integers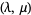 
for 
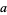and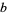 
that satisfy Bézout's identity
 |
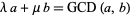are called Bézout numbers. For integers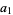 
, ..., 
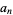, the Bézout numbers are a set of numbers 
, ..., 
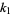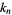such that
 |
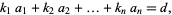where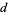 
is the greatest common divisor of 
, ..., 
.
|
|
|
|
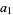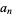دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
ناقلا تهنئة الامين العام ...وفد الأمانة العامة للعتبة العسكرية المقدسة يزور مقرات القوات الأمنية في سامراء
|
|
|
