


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 15-9-2020
Date: 30-10-2019
Date: 16-1-2021
|
There are two related conjectures, each called the twin prime conjecture. The first version states that there are an infinite number of pairs of twin primes (Guy 1994, p. 19). It is not known if there are an infinite number of such primes (Wells 1986, p. 41; Shanks 1993, p. 30), but it seems almost certain to be true. While Hardy and Wright (1979, p. 5) note that "the evidence, when examined in detail, appears to justify the conjecture," and Shanks (1993, p. 219) states even more strongly, "the evidence is overwhelming," Hardy and Wright also note that the proof or disproof of conjectures of this type "is at present beyond the resources of mathematics."
Arenstorf (2004) published a purported proof of the conjecture (Weisstein 2004). Unfortunately, a serious error was found in the proof. As a result, the paper was retracted and the twin prime conjecture remains fully open.
The conjecture that there are infinitely many Sophie Germain primes, i.e., primes 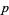 such that
such that 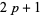 is also prime, is very closely related (Shanks 1993, p. 30).
is also prime, is very closely related (Shanks 1993, p. 30).
A second twin prime conjecture states that adding a correction proportional to 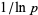 to a computation of Brun's constant ending with
to a computation of Brun's constant ending with 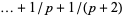 will give an estimate with error less than
will give an estimate with error less than 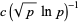 . An extended form of this conjecture, sometimes called the strong twin prime conjecture (Shanks 1993, p. 30) or first Hardy-Littlewood conjecture, states that the number
. An extended form of this conjecture, sometimes called the strong twin prime conjecture (Shanks 1993, p. 30) or first Hardy-Littlewood conjecture, states that the number 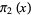 of twin primes
of twin primes 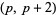 less than or equal to
less than or equal to  is asymptotically equal to
is asymptotically equal to
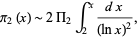 |
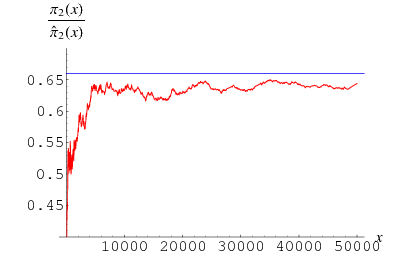
where 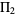 is the so-called twin primes constant (Hardy and Littlewood 1923). The value of
is the so-called twin primes constant (Hardy and Littlewood 1923). The value of 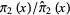 is plotted above for
is plotted above for 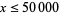 , with
, with 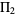 indicated in blue and taking
indicated in blue and taking 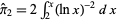 .
.
This conjecture is a special case of the more general k-tuple conjecture (also known as the first Hardy-Littlewood conjecture), which corresponds to the set 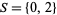 .
.
REFERENCES:
Arenstorf, R. F. "There Are Infinitely Many Prime Twins." 26 May 2004. https://arxiv.org/abs/math.NT/0405509.
Guy, R. K. "Gaps between Primes. Twin Primes." §A8 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 19-23, 1994.
Hardy, G. H. and Littlewood, J. E. "Some Problems of 'Partitio Numerorum.' III. On the Expression of a Number as a Sum of Primes." Acta Math. 44, 1-70, 1923.
Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, 1979.
Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, pp. 30-31, 2003.
Ribenboim, P. The New Book of Prime Number Records. New York: Springer-Verlag, pp. 261-265, 1996.
Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, p. 30, 1993.
Tenenbaum, G. "Re: Arenstorf's paper on the Twin Prime Conjecture." 8 Jun 2004. https://listserv.nodak.edu/scripts/wa.exe?A2=ind0406&L=nmbrthry&F=&S=&P=1119.
Weisstein, E. W. "Twin Prime Proof Proffered." MathWorld headline news, June 9, 2004. https://mathworld.wolfram.com/news/2004-06-09/twinprimes/.
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, p. 41, 1986.



|
|
|
|
حقن الذهب في العين.. تقنية جديدة للحفاظ على البصر ؟!
|
|
|
|
|
|
|
"عراب الذكاء الاصطناعي" يثير القلق برؤيته حول سيطرة التكنولوجيا على البشرية ؟
|
|
|
|
|
|
|
المجمع العلمي يعقد اجتماعاً لمناقشة إطلاق مشروع الدورات القرآنيّة الصيفيّة
|
|
|