


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 12-12-2020
Date: 31-1-2020
Date: 22-8-2020
|
Given a positive integer 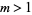 , let its prime factorization be written
, let its prime factorization be written
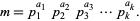 |
(1) |
Define the functions 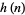 and
and 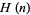 by
by 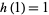 ,
, 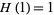 , and
, and
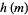 |
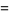 |
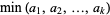 |
(2) |
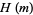 |
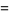 |
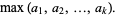 |
(3) |
The first few terms of 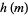 are 1, 1, 1, 2, 1, 1, 1, 3, 2, 1, 1, 1, 1, 1, 1, 4, ... (OEIS A051904), while the first few terms of
are 1, 1, 1, 2, 1, 1, 1, 3, 2, 1, 1, 1, 1, 1, 1, 4, ... (OEIS A051904), while the first few terms of 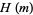 are 1, 1, 1, 2, 1, 1, 1, 3, 2, 1, 1, 2, 1, 1, 1, 4, ... (OEIS A051903).
are 1, 1, 1, 2, 1, 1, 1, 3, 2, 1, 1, 2, 1, 1, 1, 4, ... (OEIS A051903).
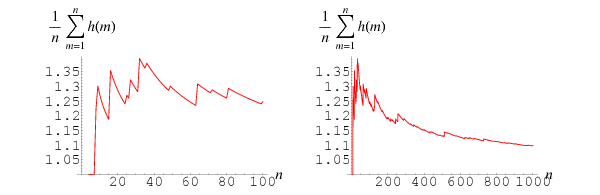
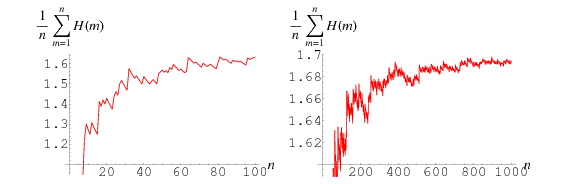
Then the average value of 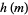 tends to
tends to
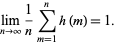 |
(4) |
Here, the running average values are given by 1/2, 2/3, 3/4, 1, 1, 1, 1, 11/9, 13/10, 14/11, 5/4, 16/13, ... (OEIS A086195 and A086196).
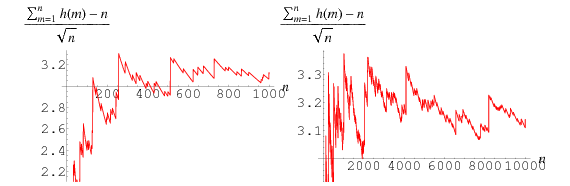
In addition, the ratio
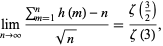 |
(5) |
where 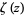 is the Riemann zeta function (Niven 1969).
is the Riemann zeta function (Niven 1969).
Niven (1969) also proved that
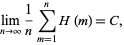 |
(6) |
where Niven's constant 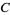 is given by
is given by
![C=1+{sum_(j=2)^infty[1-1/(zeta(j))]}=1.705211...](https://mathworld.wolfram.com/images/equations/NivensConstant/NumberedEquation5.gif) |
(7) |
(OEIS A033150). Here, the running average values are given by 1/2, 2/3, 3/4, 1, 1, 1, 1, 11/9, 13/10, 14/11, 5/4, 17/13, ... (OEIS A086197 and A086198).
The continued fraction of Niven's constant is 1, 1, 2, 2, 1, 1, 4, 1, 1, 3, 4, 4, 8, 4, 1, ... (OEIS A033151). The positions at which the digits 1, 2, ... first occur in the continued fraction are 1, 3, 10, 7, 47, 41, 34, 13, 140, 252, 20, ... (OEIS A033152). The sequence of largest terms in the continued fraction is 1, 2, 4, 8, 11, 14, 29, 372, 559, ... (OEIS A033153), which occur at positions 1, 3, 7, 13, 20, 35, 51, 68, 96, ... (OEIS A033154).
REFERENCES:
Finch, S. R. "Niven's Constant." §2.6 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 112-115, 2003.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 41, 1983.
Niven, I. "Averages of Exponents in Factoring Integers." Proc. Amer. Math. Soc. 22, 356-360, 1969.
Sloane, N. J. A. Sequences A033150, A033151, A033152, A033153, A033154, A051903, A051904, A086195, A086196, A086197, and A086198 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
دراسة تكشف "مفاجأة" غير سارة تتعلق ببدائل السكر
|
|
|
|
|
|
|
أدوات لا تتركها أبدًا في سيارتك خلال الصيف!
|
|
|
|
|
|
|
العتبة العباسية المقدسة تؤكد الحاجة لفنّ الخطابة في مواجهة تأثيرات الخطابات الإعلامية المعاصرة
|
|
|