

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Prime Products
المؤلف:
Grosswald, E
المصدر:
"Some Number Theoretical Products." Rev. Columbiana Mat. 21
الجزء والصفحة:
...
11-10-2020
1882
Prime Products
The product of primes
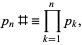 |
(1) |
with 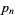 the
the 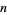 th prime, is called the primorial function, by analogy with the factorial function. Its logarithm is closely related to the Chebyshev function
th prime, is called the primorial function, by analogy with the factorial function. Its logarithm is closely related to the Chebyshev function 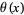 .
.
The zeta-regularized product over all primes is given by
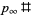 |
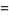 |
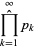 |
(2) |
 |
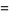 |
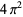 |
(3) |
(Muñoz Garcia and Pérez-Marco 2003, 2008), answering the question posed by Soulé et al. (1992, p. 101). A derivation proceeds by algebraic manipulation of the prime zeta function and gives the more general results
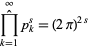 |
(4) |
and
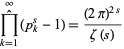 |
(5) |
(Muñoz Garcia and Pérez-Marco 2003).
Mertens theorem states that
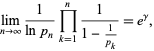 |
(6) |
where 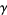 is the Euler-Mascheroni constant, and a closely related result is given by
is the Euler-Mascheroni constant, and a closely related result is given by
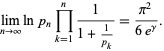 |
(7) |
There are amazing infinite product formulas for primes given by
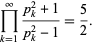 |
(8) |
(Ramanujan 1913-1914; Le Lionnais 1983, p. 46) and
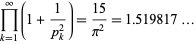 |
(9) |
(OEIS A082020; Ramanujan 1913-1914).
More general formulas are given by
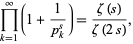 |
(10) |
where 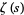 is the Riemann zeta function and by the Euler product
is the Riemann zeta function and by the Euler product
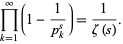 |
(11) |
Named prime products include Barban's constant
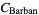 |
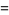 |
![product_(p)[1+(3p^2-1)/(p(p+1)(p^2-1))]](https://mathworld.wolfram.com/images/equations/PrimeProducts/Inline14.gif) |
(12) |
 |
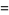 |
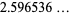 |
(13) |
(OEIS A175640), the Feller-Tornier constant
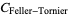 |
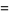 |
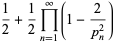 |
(14) |
 |
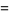 |
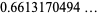 |
(15) |
(OEIS A065493), Heath-Brown-Moroz constant
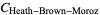 |
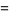 |
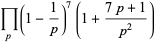 |
(16) |
 |
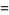 |
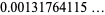 |
(17) |
(OEIS A118228), Murata's constant
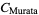 |
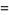 |
![product_(p)[1+1/((p-1)^2)]](https://mathworld.wolfram.com/images/equations/PrimeProducts/Inline32.gif) |
(18) |
 |
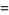 |
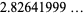 |
(19) |
(OEIS A065485), the quadratic class number constant
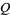 |
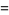 |
![product_(p)[1-1/(p^2(p+1))]](https://mathworld.wolfram.com/images/equations/PrimeProducts/Inline38.gif) |
(20) |
 |
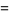 |
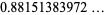 |
(21) |
(OEIS A065465), Sarnak's constant
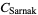 |
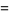 |
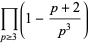 |
(22) |
 |
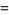 |
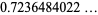 |
(23) |
(OEIS A065476), and Taniguchi's constant
 |
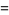 |
![product_(p)[1-3/(p^3)+2/(p^4)+1/(p^5)-1/(p^6)]](https://mathworld.wolfram.com/images/equations/PrimeProducts/Inline50.gif) |
(24) |
 |
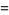 |
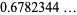 |
(25) |
(OEIS A175639), where the product is over the primes 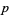 .
.
Define the number theoretic character 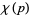 by
by
|
(26) |
then
![product_(k=2)^(infty)[1+(chi(p_k))/(p_k)]](https://mathworld.wolfram.com/images/equations/PrimeProducts/Inline56.gif) |
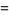 |
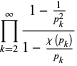 |
(27) |
 |
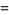 |
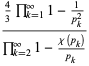 |
(28) |
 |
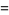 |
![4/3[zeta(2)]^(-1)L(chi,1)](https://mathworld.wolfram.com/images/equations/PrimeProducts/Inline64.gif) |
(29) |
 |
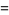 |
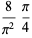 |
(30) |
 |
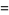 |
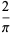 |
(31) |
 |
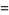 |
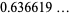 |
(32) |
(OEIS A060294; Oakes 2003). Similarly,
![product_(k=2)^(infty)[1-(chi(p_k))/(p_k)]](https://mathworld.wolfram.com/images/equations/PrimeProducts/Inline74.gif) |
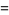 |
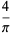 |
(33) |
 |
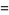 |
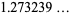 |
(34) |
(Oakes 2004). This is equivalent to the formula due to Euler
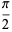 |
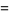 |
![product_(n=1)^(infty)[1+(sin(1/2pip_n))/(p_n)]^(-1)](https://mathworld.wolfram.com/images/equations/PrimeProducts/Inline82.gif) |
(35) |
 |
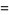 |
![product_(n=2)^(infty)[1+((-1)^((p_n-1)/2))/(p_n)]^(-1)](https://mathworld.wolfram.com/images/equations/PrimeProducts/Inline85.gif) |
(36) |
(Blatner 1997).
Let 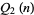 be the number of consecutive numbers
be the number of consecutive numbers 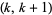 with
with 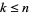 such that
such that 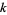 and
and 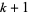 are both squarefree. Then
are both squarefree. Then 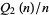 is given asymptotically by
is given asymptotically by
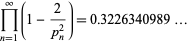 |
(37) |
(OEIS A065474), where 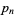 is the
is the 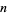 th prime.
th prime.
REFERENCES:
Blatner, D. The Joy of Pi. New York: Walker, p. 110, 1997.
Grosswald, E. "Some Number Theoretical Products." Rev. Columbiana Mat. 21, 231-242, 1987.
Guy, R. K. "Products Taken over Primes." §B87 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 102-103, 1994.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 46, 1983.
Muñoz García, E. and Pérez Marco, R. "The Product Over All Primes is 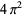 ." Preprint IHES/M/03/34. May 2003. https://inc.web.ihes.fr/prepub/PREPRINTS/M03/Resu/resu-M03-34.html.
." Preprint IHES/M/03/34. May 2003. https://inc.web.ihes.fr/prepub/PREPRINTS/M03/Resu/resu-M03-34.html.
Muñoz García, E. and Pérez Marco, R. "The Product Over All Primes is 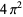 ." Commun. Math. Phys. 277, 69-81, 2008.
." Commun. Math. Phys. 277, 69-81, 2008.
Niklasch, G. "Some Number-Theoretical Constants Arising as Products of Rational Functions of 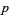 over the Primes." https://www.gn-50uma.de/alula/essays/Moree/Moree.en.shtml.
over the Primes." https://www.gn-50uma.de/alula/essays/Moree/Moree.en.shtml.
Oakes, M. "Re: [PrimeNumbers] pi=(2/1) (3/2) (5/6) (7/6) (11/10) (13/14) (17/18) (19/18)...." Dec. 21, 2003. https://groups.yahoo.com/group/primenumbers/message/14257.
Oakes, M. "Re: primes and pi." Jan. 29, 2004. https://groups.yahoo.com/group/primenumbers/message/14486.
Ramanujan, S. "Modular Equations and Approximations to 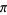 ." Quart. J. Pure. Appl. Math. 45, 350-372, 1913-1914.
." Quart. J. Pure. Appl. Math. 45, 350-372, 1913-1914.
Sloane, N. J. A. Sequences A065465, A065474, A065485, A065493, A082020, A118228, A175639, and A175640 in "The On-Line Encyclopedia of Integer Sequences."
Soulé, C.; Abramovich, D.; Burnois, J. F.; and Kramer, J. Lectures on Arakelov Geometry. Cambridge, England: Cambridge University Press, 1992.
Uchiyama, S. "On Some Products Involving Primes." Proc. Amer. Math. Soc. 28, 629-630, 1971.
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام) قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)
قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى) قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)
قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)


















