An infinite sequence of positive integers 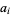 satisfying

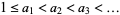(1)

is an 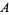-sequence if no  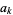is the sum of two or more distinct earlier terms (Guy 1994). Such sequences are sometimes also known as sum-free sets.

Erdős (1962) proved

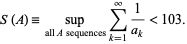(2)

Any 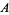-sequence satisfies the chi inequality (Levine and O'Sullivan 1977), which gives 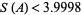. Abbott (1987) and Zhang (1992) have given a bound from below, so the best result to date is

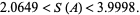(3)

Levine and O'Sullivan (1977) conjectured that the sum of reciprocals of an 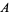-sequence satisfies

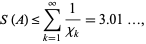(4)

where 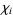 are given by the Levine-O'Sullivan greedy algorithm. However, summing the first  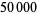terms of the Levine-O'Sullivan sequence already gives 3.0254....

REFERENCES:

Abbott, H. L. "On Sum-Free Sequences." Acta Arith. 48, 93-96, 1987.

Erdős, P. "Remarks on Number Theory III. Some Problems in Additive Number Theory." Mat. Lapok 13, 28-38, 1962.

Finch, S. R. "Erdős' Reciprocal Sum Constants." §2.20 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 163-166, 2003.

Guy, R. K. "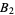-Sequences." §E28 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 228-229, 1994.

Levine, E. and O'Sullivan, J. "An Upper Estimate for the Reciprocal Sum of a Sum-Free Sequence." Acta Arith. 34, 9-24, 1977.

Zhang, Z. X. "A Sum-Free Sequence with Larger Reciprocal Sum." Unpublished manuscript, 1992.

اخر الاخبار

اخبار العتبة العباسية المقدسة

المجمَع العلمي يطلق الدورة التطويرية الخامسة لمعلمي التربية الإسلامية ومدرسيها في النجف الأشرف

خدمات إنسانية متنوّعة تقدّمها شعبة الشهداء والجرحى في مختلف المحافظات

قسم العلاقات العامة يطلق فعاليات مخيم البذرة الواعدة الخاص بأبناء المنتسبين

جامعة العميد تنظم سلسلة دورات تطويرية لملاكاتها الإدارية

المزيد

الآخبار الصحية

اختراق علمي.. دواء يؤخر ظهور السكري من النوع الأول لسنوات

هذا ما يحدث لجسمك إن أهملت نظافة فراشك

لماذا تعتبر النساء أكثر عرضة للإصابة بألزهايمر من الرجال؟

لماذا يحذر الخبراء من الإفراط في تناول الفراولة؟

المزيد

الآخبار التكنلوجية

السيارات الكهربائية أنظف بنسبة 73% من سيارات الوقود

سيارة لوسِد الكهربائية تدخل "غينيس" بأطول مدى في العالم

نظرية جديدة تنسف كل ما نعرفه عن تشكل أول قارة في الأرض

منذ 37 ألف عام.. دراسة تكشف "أقدم أمراض" أصابت البشر

المزيد