


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 18-12-2019
Date: 17-11-2020
Date: 19-3-2020
|
The limiting rabbit sequence written as a binary fraction 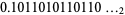 (OEIS A005614), where
(OEIS A005614), where 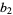 denotes a binary number (a number in base-2). The decimal value is
denotes a binary number (a number in base-2). The decimal value is
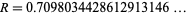 |
(1) |
(OEIS A014565).
Amazingly, the rabbit constant is also given by the continued fraction [0; 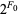 ,
, 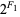 ,
, 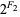 ,
, 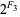 , ...] = [2, 2, 4, 8, 32, 256, 8192, 2097152, 17179869184, ...] (OEIS A000301), where
, ...] = [2, 2, 4, 8, 32, 256, 8192, 2097152, 17179869184, ...] (OEIS A000301), where 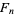 are Fibonacci numbers with
are Fibonacci numbers with 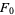 taken as 0 (Gardner 1989, Schroeder 1991). Another amazing connection was discovered by S. Plouffe. Define the Beatty sequence
taken as 0 (Gardner 1989, Schroeder 1991). Another amazing connection was discovered by S. Plouffe. Define the Beatty sequence 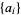 by
by
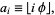 |
(2) |
where 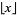 is the floor function and
is the floor function and 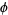 is the golden ratio. The first few terms are 1, 3, 4, 6, 8, 9, 11, ... (OEIS A000201). Then
is the golden ratio. The first few terms are 1, 3, 4, 6, 8, 9, 11, ... (OEIS A000201). Then
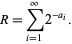 |
(3) |
This is a special case of the Devil's staircase function with 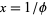 .
.
The irrationality measure of 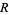 is
is 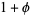 (D. Terr, pers. comm., May 21, 2004).
(D. Terr, pers. comm., May 21, 2004).
REFERENCES:
Anderson, P. G.; Brown, T. C.; and Shiue, P. J.-S. "A Simple Proof of a Remarkable Continued Fraction Identity." Proc. Amer. Math. Soc. 123, 2005-2009, 1995.
Finch, S. R. "Prouhet-Thue-Morse Constant." §6.8 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 436-441, 2003.
Gardner, M. Penrose Tiles and Trapdoor Ciphers... and the Return of Dr. Matrix, reissue ed. New York: W. H. Freeman, pp. 21-22, 1989.
Schroeder, M. Fractals, Chaos, Power Laws: Minutes from an Infinite Paradise. New York: W. H. Freeman, p. 55, 1991.
Sloane, N. J. A. Sequences A000301, A000201/M2322, A005614, and A014565 in "The On-Line Encyclopedia of Integer Sequences."a



|
|
|
|
دراسة تكشف "مفاجأة" غير سارة تتعلق ببدائل السكر
|
|
|
|
|
|
|
أدوات لا تتركها أبدًا في سيارتك خلال الصيف!
|
|
|
|
|
|
|
العتبة العباسية المقدسة تؤكد الحاجة لفنّ الخطابة في مواجهة تأثيرات الخطابات الإعلامية المعاصرة
|
|
|