
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 27-3-2021
Date: 15-2-2016
Date: 6-3-2021
|
Given an event 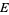 in a sample space
in a sample space 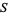 which is either finite with
which is either finite with 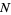 elements or countably infinite with
elements or countably infinite with 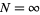 elements, then we can write
elements, then we can write
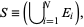 |
and a quantity 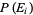 , called the probability of event
, called the probability of event 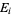 , is defined such that
, is defined such that
1. 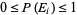 .
.
2. 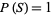 .
.
3. Additivity: 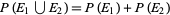 , where
, where 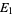 and
and 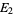 are mutually exclusive.
are mutually exclusive.
4. Countable additivity: 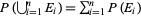 for
for 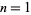 , 2, ...,
, 2, ..., 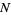 where
where 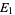 ,
, 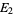 , ... are mutually exclusive (i.e.,
, ... are mutually exclusive (i.e., 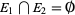 ).
).
REFERENCES:
Doob, J. L. "The Development of Rigor in Mathematical Probability (1900-1950)." Amer. Math. Monthly 103, 586-595, 1996.
Papoulis, A. Probability, Random Variables, and Stochastic Processes, 2nd ed. New York: McGraw-Hill, pp. 26-28, 1984.



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|