المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Least Squares Fitting--Exponential |
 1493
 03:49 مساءً
date: 28-3-2021 |
Author : المرجع الالكتروني للمعلوماتيه 
Book or Source : www.almerja.com 
Page and Part : ...|
Read More
Date: 10-4-2021
1644
Date: 24-2-2021
2205
Date: 13-2-2021
1294
|
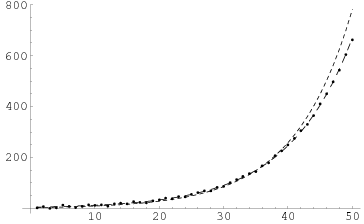
To fit a functional form
 |
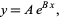(1) |
take the logarithm of both sides
 |
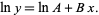(2) |
The best-fit values are then
 |
 |
 |
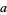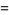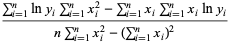(3) |
 |
 |
 |
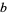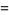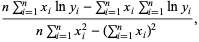(4) |
where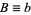 
and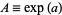 
.
This fit gives greater weights to small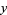 
values so, in order to weight the points equally, it is often better to minimize the function
 |
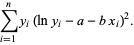(5) |
Applying least squares fitting gives
 |
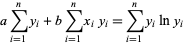(6) |
 |
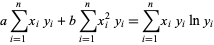(7) |
![[sum_(i=1)^(n)y_i sum_(i=1)^(n)x_iy_i; sum_(i=1)^(n)x_iy_i sum_(i=1)^(n)x_i^2y_i][a; b]=[sum_(i=1)^(n)y_ilny_i; sum_(i=1)^(n)x_iy_ilny_i].](https://mathworld.wolfram.com/images/equations/LeastSquaresFittingExponential/NumberedEquation6.gif) |
(8) |
Solving for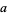 
and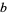 
,
 |
 |
 |
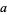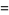(9) |
 |
 |
 |
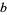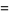(10) |
In the plot above, the short-dashed curve is the fit computed from (◇) and (◇) and the long-dashed curve is the fit computed from (9) and (10).
|
|
|
|
هل تعرف كيف يؤثر الطقس على ضغط إطارات سيارتك؟ إليك الإجابة
|
|
|
|
|
|
|
العتبة العباسية المقدسة تواصل إقامة مجالس العزاء بذكرى شهادة الإمام الكاظم (عليه السلام)
|
|
|
