


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 15-3-2021
Date: 18-3-2021
Date: 26-4-2021
|
An 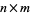 matrix
matrix 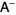 is a 1-inverse of an
is a 1-inverse of an 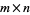 matrix
matrix 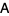 for which
for which
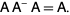 |
(1) |
The Moore-Penrose matrix inverse is a particular type of 1-inverse.
A matrix equation
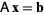 |
(2) |
has a solution iff
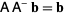 |
(3) |
(Campbell and Meyer 1991).
Let 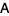 be an
be an 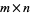 matrix and use elementary row operations (through premultiplication by a nonsingular matrix
matrix and use elementary row operations (through premultiplication by a nonsingular matrix 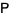 obtained by performing the same operations on the identity matrix) and elementary column operations (through postmultiplication by a nonsingular matrix
obtained by performing the same operations on the identity matrix) and elementary column operations (through postmultiplication by a nonsingular matrix 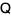 obtained by performing the same operations on the identity matrix) to transform
obtained by performing the same operations on the identity matrix) to transform 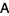 into the form
into the form
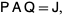 |
(4) |
where 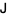 is the block matrix
is the block matrix
![J=[I 0; 0 0]](https://mathworld.wolfram.com/images/equations/Matrix1-Inverse/NumberedEquation5.gif) |
(5) |
and 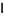 is an
is an 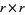 identity matrix with
identity matrix with 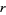 the rank of
the rank of 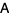 . Then a matrix
. Then a matrix 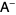 is a 1-inverse of
is a 1-inverse of 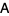 iff there are appropriately dimensional matrices
iff there are appropriately dimensional matrices 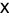 ,
, 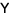 and
and 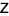 such that
such that
![A^-=Q[I X; Y Z]P](https://mathworld.wolfram.com/images/equations/Matrix1-Inverse/NumberedEquation6.gif) |
(6) |
(Jodár et al. 1991).
REFERENCES:
Campbell, S. L. and Meyer, C. D. Jr. Generalized Inverses of Linear Transformations. New York: Dover, 1991.
Jodár, L.; Law, A. G.; Rezazadeh, A.; Watson, J. H.; and Wu, G. "Computations for the Moore-Penrose and Other Generalized Inverses." Congress. Numer. 80, 57-64, 1991.
Rao, C. R. and Mitra, S. K. Generalized Inverse of Matrices and Its Applications. New York: Wiley, 1971.



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
ناقلا تهنئة الامين العام ...وفد الأمانة العامة للعتبة العسكرية المقدسة يزور مقرات القوات الأمنية في سامراء
|
|
|