


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 11-3-2021
Date: 13-4-2021
Date: 8-2-2021
|
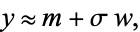 |
(1) |
where
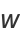 |
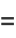 |
![x+[gamma_1h_1(x)]+[gamma_2h_2(x)+gamma_1^2h_(11)(x)]+[gamma_3h_3(x)+gamma_1gamma_2h_(12)(x)+gamma_1^3h_(111)(x)]+[gamma_4h_4(x)+gamma_2^2h_(22)(x)+gamma_1gamma_3h_(13)(x)+gamma_1^2gamma_2h_(112)(x)+gamma_1^4h_(1111)(x)]+...,](https://mathworld.wolfram.com/images/equations/Cornish-FisherAsymptoticExpansion/Inline3.gif) |
(2) |
where
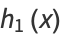 |
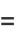 |
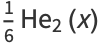 |
(3) |
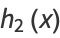 |
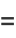 |
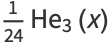 |
(4) |
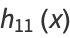 |
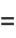 |
![-1/(36)[2He_3(x)+He_1(x)]](https://mathworld.wolfram.com/images/equations/Cornish-FisherAsymptoticExpansion/Inline12.gif) |
(5) |
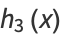 |
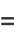 |
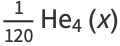 |
(6) |
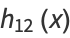 |
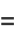 |
![-1/(24)[He_4(x)+He_2(x)]](https://mathworld.wolfram.com/images/equations/Cornish-FisherAsymptoticExpansion/Inline18.gif) |
(7) |
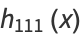 |
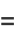 |
![1/(324)[12He_4(x)+19He_2(x)]](https://mathworld.wolfram.com/images/equations/Cornish-FisherAsymptoticExpansion/Inline21.gif) |
(8) |
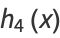 |
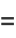 |
 |
(9) |
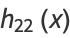 |
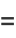 |
![-1/(384)[3He_5(x)+6He_3(x)+2He_1(x)]](https://mathworld.wolfram.com/images/equations/Cornish-FisherAsymptoticExpansion/Inline27.gif) |
(10) |
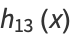 |
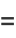 |
![-1/(180)[2He_5+3He_3(x)]](https://mathworld.wolfram.com/images/equations/Cornish-FisherAsymptoticExpansion/Inline30.gif) |
(11) |
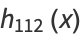 |
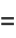 |
![1/(288)[14He_5(x)+37He_3(x)+8He_1(x)]](https://mathworld.wolfram.com/images/equations/Cornish-FisherAsymptoticExpansion/Inline33.gif) |
(12) |
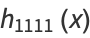 |
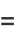 |
![-1/(7776)[252He_5(x)+832He_3(x)+227He_1(x)]](https://mathworld.wolfram.com/images/equations/Cornish-FisherAsymptoticExpansion/Inline36.gif) |
(13) |
and combinations of Hermite polynomials.
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 935, 1972.
Cornish, E. A. and Fisher, R. A. "Moments and Cumulants in the Specification of Distributions." Extrait de la Revue de l'Institute International de Statistique 4, 1-14, 1937. Reprinted in Fisher, R. A. Contributions to Mathematical Statistics. New York: Wiley, 1950.
Wallace, D. L. "Asymptotic Approximations to Distributions." Ann. Math. Stat. 29, 635-654, 1958.
Wasow, W. "On the Asymptotic Transformation of Certain Distributions into the Normal Distribution." Proceedings of Symposia in Applied Mathematica VI, Numerical Analysis. New York: McGraw-Hill, pp. 251-259, 1956.



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
الأمين العام للعتبة العسكرية المقدسة يستقبل مدير الوقف الجعفري في دولة الكويت
|
|
|