المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Bundle Rank |
 1426
 04:02 مساءً
date: 23-5-2021 |
Author : المرجع الالكتروني للمعلوماتيه 
Book or Source : www.almerja.com 
Page and Part : ...|
Read More
Date: 14-7-2021
1579
Date: 15-5-2021
1597
Date: 4-8-2021
2492
|
The rank of a vector bundle is the dimension of its fiber. Equivalently, it is the maximum number of linearly independent local bundle sections in a trivialization. Naturally, the dimension here is measured in the appropriate category. For instance, a real line bundle has fibers isomorphic with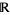 
, and a complex line bundle has fibers isomorphic to 
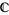, but in both cases their rank is 1.
The rank of the tangent bundle of a real manifold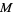 
is equal to the dimension of 
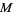. The rank of a trivial bundle 
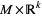is equal to 
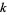. There is no upper bound to the rank of a vector bundle over a fixed manifold 
.
|
|
|
|
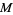دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|
