
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 2-7-2017
Date: 5-8-2021
Date: 22-6-2021
|
A complex line bundle is a vector bundle 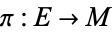 whose fibers
whose fibers 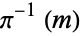 are a copy of
are a copy of 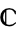 .
. 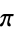 is a holomorphic line bundle if it is a holomorphic map between complex manifolds and its transition functions are holomorphic.
is a holomorphic line bundle if it is a holomorphic map between complex manifolds and its transition functions are holomorphic.
 |
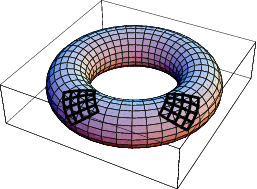 |
On a compact Riemann surface, a variety divisor 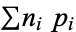 determines a line bundle. For example, consider
determines a line bundle. For example, consider 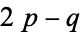 on
on 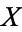 . Around
. Around 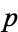 there is a coordinate chart
there is a coordinate chart 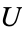 given by the holomorphic function
given by the holomorphic function 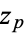 with
with 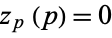 . Similarly,
. Similarly, 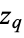 is a holomorphic function defining a disjoint chart
is a holomorphic function defining a disjoint chart  around
around  with
with 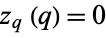 . Then letting
. Then letting 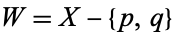 , the Riemann surface is covered by
, the Riemann surface is covered by 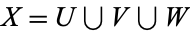 . The line bundle corresponding to
. The line bundle corresponding to 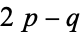 is then defined by the following transition functions,
is then defined by the following transition functions,
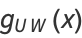 |
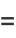 |
 |
(1) |
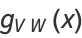 |
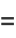 |
 |



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|