

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Topology
المؤلف:
Adamson, I.
المصدر:
A General Topology Workbook. Boston, MA: Birkhäuser, 1996.
الجزء والصفحة:
...
3-6-2021
4275
Topology
Topology is the mathematical study of the properties that are preserved through deformations, twistings, and stretchings of objects. Tearing, however, is not allowed. A circle is topologically equivalent to an ellipse (into which it can be deformed by stretching) and a sphere is equivalent to an ellipsoid. Similarly, the set of all possible positions of the hour hand of a clock is topologically equivalent to a circle (i.e., a one-dimensional closed curve with no intersections that can be embedded in two-dimensional space), the set of all possible positions of the hour and minute hands taken together is topologically equivalent to the surface of a torus (i.e., a two-dimensional a surface that can be embedded in three-dimensional space), and the set of all possible positions of the hour, minute, and second hands taken together are topologically equivalent to a three-dimensional object.
The definition of topology leads to the following mathematical joke (Renteln and Dundes 2005):
Q: What is a topologist? A: Someone who cannot distinguish between a doughnut and a coffee cup.
There is more to topology, though. Topology began with the study of curves, surfaces, and other objects in the plane and three-space. One of the central ideas in topology is that spatial objects like circles and spheres can be treated as objects in their own right, and knowledge of objects is independent of how they are "represented" or "embedded" in space. For example, the statement "if you remove a point from a circle, you get a line segment" applies just as well to the circle as to an ellipse, and even to tangled or knotted circles, since the statement involves only topological properties.
Topology has to do with the study of spatial objects such as curves, surfaces, the space we call our universe, the space-time of general relativity, fractals, knots, manifolds (which are objects with some of the same basic spatial properties as our universe), phase spaces that are encountered in physics (such as the space of hand-positions of a clock), symmetry groups like the collection of ways of rotating a top, etc.

Topology can be used to abstract the inherent connectivity of objects while ignoring their detailed form. For example, the figures above illustrate the connectivity of a number of topologically distinct surfaces. In these figures, parallel edges drawn in solid join one another with the orientation indicated with arrows, so corners labeled with the same letter correspond to the same point, and dashed lines show edges that remain free (Gardner 1971, pp. 15-17; Gray 1997, pp. 322-324). The above figures correspond to the disk (plane), Klein bottle, Möbius strip, real projective plane, sphere, torus, and tube. The labels are often omitted in such diagrams since they are implied by connection of parallel lines with the orientations indicated by the arrows.
The "objects" of topology are often formally defined as topological spaces. If two objects have the same topological properties, they are said to be homeomorphic (although, strictly speaking, properties that are not destroyed by stretching and distorting an object are really properties preserved by isotopy, not homeomorphism; isotopy has to do with distorting embedded objects, while homeomorphism is intrinsic).
Around 1900, Poincaré formulated a measure of an object's topology, called homotopy (Collins 2004). In particular, two mathematical objects are said to be homotopic if one can be continuously deformed into the other.
Topology can be divided into algebraic topology (which includes combinatorial topology), differential topology, and low-dimensional topology. The low-level language of topology, which is not really considered a separate "branch" of topology, is known as point-set topology.
There is also a formal definition for a topology defined in terms of set operations. A set 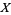 along with a collection
along with a collection 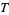 of subsets of it is said to be a topology if the subsets in
of subsets of it is said to be a topology if the subsets in 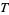 obey the following properties:
obey the following properties:
1. The (trivial) subsets 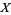 and the empty set
and the empty set 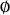 are in
are in 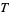 .
.
2. Whenever sets 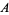 and
and 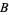 are in
are in 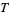 , then so is
, then so is 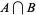 .
.
3. Whenever two or more sets are in 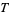 , then so is their union
, then so is their union
(Bishop and Goldberg 1980). This definition can be used to enumerate the topologies on 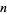 symbols. For example, the unique topology of order 1 is
symbols. For example, the unique topology of order 1 is {emptyset,{1}}" src="https://mathworld.wolfram.com/images/equations/Topology/Inline13.gif" style="height:15px; width:45px" />, while the four topologies of order 2 are
{emptyset,{1},{1,2}}" src="https://mathworld.wolfram.com/images/equations/Topology/Inline14.gif" style="height:15px; width:85px" />,
{emptyset,{1,2}}" src="https://mathworld.wolfram.com/images/equations/Topology/Inline15.gif" style="height:15px; width:60px" />,
{emptyset,{1,2},{2}}" src="https://mathworld.wolfram.com/images/equations/Topology/Inline16.gif" style="height:15px; width:85px" />, and
{emptyset,{1},{2},{1,2}}" src="https://mathworld.wolfram.com/images/equations/Topology/Inline17.gif" style="height:15px; width:110px" />. The numbers of topologies on sets of cardinalities
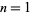 , 2, ... are 1, 4, 29, 355, 6942, ... (OEIS A000798).
, 2, ... are 1, 4, 29, 355, 6942, ... (OEIS A000798).
A set 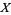 for which a topology
for which a topology 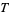 has been specified is called a topological space (Munkres 2000, p. 76). For example, the set
has been specified is called a topological space (Munkres 2000, p. 76). For example, the set {1,2,3,4}" src="https://mathworld.wolfram.com/images/equations/Topology/Inline21.gif" style="height:15px; width:90px" /> together with the subsets
{emptyset,{1},{2,3,4},{1,2,3,4}}" src="https://mathworld.wolfram.com/images/equations/Topology/Inline22.gif" style="height:15px; width:196px" /> comprises a topology, and
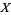 is a topological space.
is a topological space.
Topologies can be built up from topological bases. For the real numbers, a topological basis is the set of open intervals.
REFERENCES:
Adamson, I. A General Topology Workbook. Boston, MA: Birkhäuser, 1996.
Alexandrov, P. S. Elementary Concepts of Topology. New York: Dover, 1961.
Armstrong, M. A. Basic Topology, rev. ed. New York: Springer-Verlag, 1997.
Arnold, B. H. Intuitive Concepts in Elementary Topology. New York: Prentice-Hall, 1962.
Barr, S. Experiments in Topology. New York: Dover, 1964.
Berge, C. Topological Spaces Including a Treatment of Multi-Valued Functions, Vector Spaces and Convexity. New York: Dover, 1997.
Bishop, R. and Goldberg, S. Tensor Analysis on Manifolds. New York: Dover, 1980.
Blackett, D. W. Elementary Topology: A Combinatorial and Algebraic Approach. New York: Academic Press, 1967.
Bloch, E. A First Course in Geometric Topology and Differential Geometry. Boston, MA: Birkhäuser, 1996.
Brown, J. I. and Watson, S. "The Number of Complements of a Topology on 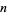 Points is at Least
Points is at Least 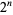 (Except for Some Special Cases)." Discr. Math. 154, 27-39, 1996.
(Except for Some Special Cases)." Discr. Math. 154, 27-39, 1996.
Chinn, W. G. and Steenrod, N. E. First Concepts of Topology: The Geometry of Mappings of Segments, Curves, Circles, and Disks. Washington, DC: Math. Assoc. Amer., 1966.
Collins, G. P. "The Shapes of Space." Sci. Amer. 291, 94-103, July 2004.
Comtet, L. Advanced Combinatorics: The Art of Finite and Infinite Expansions, rev. enl. ed. Dordrecht, Netherlands: Reidel, p. 229, 1974.
Dugundji, J. Topology. Englewood Cliffs, NJ: Prentice-Hall, 1965.
Eppstein, D. "Geometric Topology." https://www.ics.uci.edu/~eppstein/junkyard/topo.html.
Erné, M. and Stege, K. "Counting Finite Posets and Topologies." Order 8, 247-265, 1991.
Evans, J. W.; Harary, F.; and Lynn, M. S. "On the Computer Enumeration of Finite Topologies." Commun. ACM 10, 295-297 and 313, 1967.
Francis, G. K. A Topological Picturebook. New York: Springer-Verlag, 1987.
Gardner, M. Martin Gardner's Sixth Book of Mathematical Games from Scientific American. New York: Scribner's, 1971.
Gemignani, M. C. Elementary Topology. New York: Dover, 1990.
Gray, A. Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, 1997.
Greever, J. Theory and Examples of Point-Set Topology. Belmont, CA: Brooks/Cole, 1967.
Heitzig, J. and Reinhold, J. "The Number of Unlabeled Orders on Fourteen Elements." Preprint No. 299. Hanover, Germany: Universität Hannover Institut für Mathematik, 1999.
Hirsch, M. W. Differential Topology. New York: Springer-Verlag, 1988.
Hocking, J. G. and Young, G. S. Topology. New York: Dover, 1988.
Kahn, D. W. Topology: An Introduction to the Point-Set and Algebraic Areas. New York: Dover, 1995.
Kelley, J. L. General Topology. New York: Springer-Verlag, 1975.
Kinsey, L. C. Topology of Surfaces. New York: Springer-Verlag, 1993.
Kleitman, D. and Rothschild, B. L. "The Number of Finite Topologies." Proc. Amer. Math. Soc. 25, 276-282, 1970.
Lietzmann, W. Visual Topology. London: Chatto and Windus, 1965.
Lipschutz, S. Theory and Problems of General Topology. New York: Schaum, 1965.
Mendelson, B. Introduction to Topology. New York: Dover, 1990.
Munkres, J. R. Elementary Differential Topology. Princeton, NJ: Princeton University Press, 1963.
Munkres, J. R. Topology: A First Course, 2nd ed. Upper Saddle River, NJ: Prentice-Hall, 2000.
Oliver, D. "GANG Library." https://www.gang.umass.edu/library/library_home.html.
Praslov, V. V. and Sossinsky, A. B. Knots, Links, Braids and 3-Manifolds: An Introduction to the New Invariants in Low-Dimensional Topology. Providence, RI: Amer. Math. Soc., 1996.
Rayburn, M. "On the Borel Fields of a Finite Set." Proc. Amer. Math. Soc. 19, 885-889, 1968.
Renteln, P. and Dundes, A. "Foolproof: A Sampling of Mathematical Folk Humor." Notices Amer. Math. Soc. 52, 24-34, 2005.
Seifert, H. and Threlfall, W. A Textbook of Topology. New York: Academic Press, 1980.
Shafaat, A. "On the Number of Topologies Definable for a Finite Set." J. Austral. Math. Soc. 8, 194-198, 1968.
Shakhmatv, D. and Watson, S. "Topology Atlas." https://at.yorku.ca/topology/.
Sloane, N. J. A. Sequence A000798/M3631 in "The On-Line Encyclopedia of Integer Sequences."
Steen, L. A. and Seebach, J. A. Jr. Counterexamples in Topology. New York: Dover, 1996.
Thurston, W. P. Three-Dimensional Geometry and Topology, Vol. 1. Princeton, NJ: Princeton University Press, 1997.
Tucker, A. W. and Bailey, H. S. Jr. "Topology." Sci. Amer. 182, 18-24, Jan. 1950.
van Mill, J. and Reed, G. M. (Eds.). Open Problems in Topology. New York: Elsevier, 1990.
Veblen, O. Analysis Situs, 2nd ed. New York: Amer. Math. Soc., 1946.
Weisstein, E. W. "Books about Topology." https://www.ericweisstein.com/encyclopedias/books/Topology.html.
 الاكثر قراءة في التبلوجيا
الاكثر قراءة في التبلوجيا
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام) قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)
قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى) قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)
قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)


















