المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Hamiltonian Map |
 830
 02:39 صباحاً
date: 7-10-2021 |
Author : المرجع الالكتروني للمعلوماتيه 
Book or Source : www.almerja.com 
Page and Part : ...|
Read More
Date: 21-12-2021
1746
Date: 21-8-2021
1657
Date: 7-10-2021
1501
|
Consider a one-dimensional Hamiltonian map of the form
 |
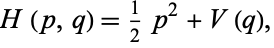(1) |
which satisfies Hamilton's equations
 |
 |
 |
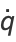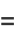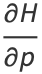(2) |
 |
 |
 |
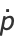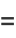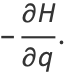(3) |
Now, write
 |
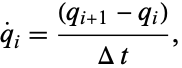(4) |
where
 |
 |
 |
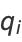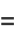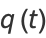(5) |
 |
 |
 |
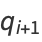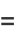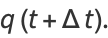(6) |
Then the equations of motion become
 |
 |
 |
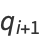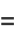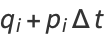(7) |
 |
 |
 |
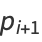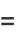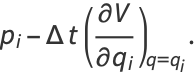(8) |
Note that equations (7) and (8) are not area-preserving, since
 |
 |
 |
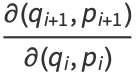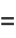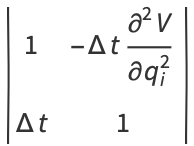(9) |
 |
 |
 |
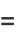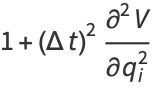(10) |
 |
 |
 |
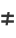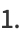(11) |
However, if we take instead of (9) and (10),
 |
 |
 |
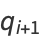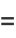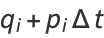(12) |
 |
 |
 |
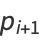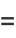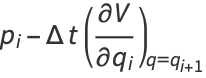(13) |
 |
 |
 |
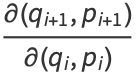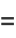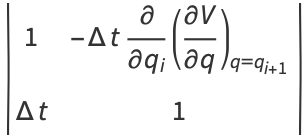(14) |
 |
 |
 |
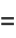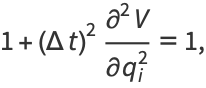(15) |
which is area-preserving.
|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|
