


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 9-2-2016
Date: 24-11-2021
Date: 19-10-2021
|
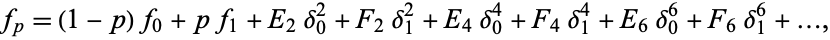 |
(1) |
for ![p in [0,1]](https://mathworld.wolfram.com/images/equations/EverettsFormula/Inline1.gif) , where
, where 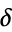 is the central difference and
is the central difference and
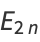 |
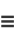 |
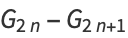 |
(2) |
 |
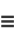 |
 |
(3) |
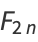 |
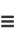 |
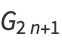 |
(4) |
 |
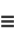 |
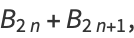 |
(5) |
where 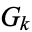 are the coefficients from Gauss's backward formula and Gauss's forward formula and
are the coefficients from Gauss's backward formula and Gauss's forward formula and 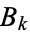 are the coefficients from Bessel's finite difference formula. The
are the coefficients from Bessel's finite difference formula. The 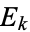 s and
s and 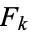 s also satisfy
s also satisfy
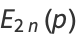 |
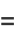 |
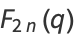 |
(6) |
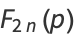 |
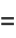 |
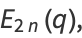 |
(7) |
for
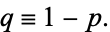 |
(8) |
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 880-881, 1972.
Acton, F. S. Numerical Methods That Work, 2nd printing. Washington, DC: Math. Assoc. Amer., pp. 92-93, 1990.
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 433, 1987.
Whittaker, E. T. and Robinson, G. "The Laplace-Everett Formula." §25 in The Calculus of Observations: A Treatise on Numerical Mathematics, 4th ed. New York: Dover, pp. 40-41, 1967.



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|