


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 14-12-2021
Date: 5-12-2021
Date: 14-12-2021
|
Chebyshev-Gauss quadrature, also called Chebyshev quadrature, is a Gaussian quadrature over the interval ![[-1,1]](https://mathworld.wolfram.com/images/equations/Chebyshev-GaussQuadrature/Inline1.gif) with weighting function
with weighting function 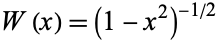 (Abramowitz and Stegun 1972, p. 889). The abscissas for quadrature order
(Abramowitz and Stegun 1972, p. 889). The abscissas for quadrature order 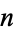 are given by the roots of the Chebyshev polynomial of the first kind
are given by the roots of the Chebyshev polynomial of the first kind 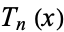 , which occur symmetrically about 0. The weights are
, which occur symmetrically about 0. The weights are
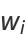 |
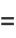 |
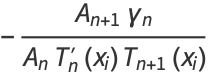 |
(1) |
 |
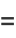 |
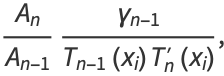 |
(2) |
where 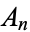 is the coefficient of
is the coefficient of 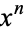 in
in 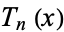 ,
,
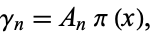 |
(3) |
and 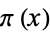 the order-
the order-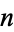 Lagrange interpolating polynomial for
Lagrange interpolating polynomial for 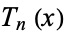 .
.
For Chebyshev polynomials of the first kind,
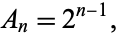 |
(4) |
so
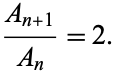 |
(5) |
Additionally,
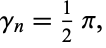 |
(6) |
so
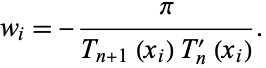 |
(7) |
Since
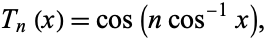 |
(8) |
the abscissas are given explicitly by
![x_i=cos[((2i-1)pi)/(2n)].](https://mathworld.wolfram.com/images/equations/Chebyshev-GaussQuadrature/NumberedEquation7.gif) |
(9) |
Since
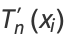 |
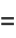 |
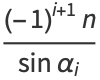 |
(10) |
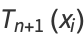 |
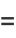 |
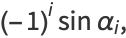 |
(11) |
where
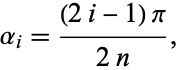 |
(12) |
all the weights are
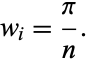 |
(13) |
The explicit formula is then
![int_(-1)^1(f(x)dx)/(sqrt(1-x^2))=pi/nsum_(k=1)^nf[cos((2k-1)/(2n)pi)]+(2pi)/(2^(2n)(2n)!)f^((2n))(xi).](https://mathworld.wolfram.com/images/equations/Chebyshev-GaussQuadrature/NumberedEquation10.gif) |
(14) |
The following two tables give the numerical and analytic values for the first few points and weights.
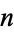 |
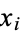 |
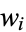 |
| 2 | 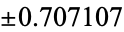 |
1.5708 |
| 3 | 0 | 1.0472 |
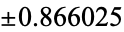 |
1.0472 | |
| 4 | 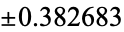 |
0.785398 |
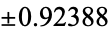 |
0.785398 | |
| 5 | 0 | 0.628319 |
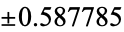 |
0.628319 | |
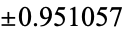 |
0.628319 |
| 2 | 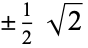 |
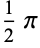 |
| 3 | 0 | 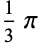 |
| 3 | 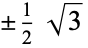 |
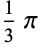 |
| 4 | 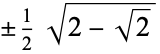 |
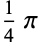 |
| 4 | 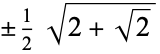 |
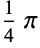 |
| 5 | 0 | 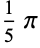 |
| 5 | 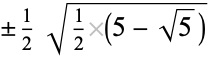 |
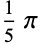 |
| 5 | 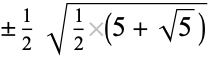 |
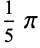 |
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 889, 1972.
Bronwin, B. "On the Determination of the Coefficients in Any Series of Sines and Cosines of Multiples of a Variable Angle from Particular Values of that Series." Phil. Mag. 34, 260-268, 1849.
Hildebrand, F. B. Introduction to Numerical Analysis. New York: McGraw-Hill, pp. 330-331, 1956.
Tchebicheff, P. "Sur les quadratures." J. de math. pures appliq. 19, 19-34, 1874.
Whittaker, E. T. and Robinson, G. "Chebyshef's Formulae." §79 in The Calculus of Observations: A Treatise on Numerical Mathematics, 4th ed. New York: Dover, pp. 158-159, 1967.



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|