المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | منحني تكراري رائي J- Shaped Curve |
 2220
 02:27 صباحاً
التاريخ: 20-12-2015 |
المؤلف : صالح رشيد بطارسه 
الكتاب أو المصدر : معجم الرياضيات 
الجزء والصفحة : 338-339|
أقرأ أيضاً
التاريخ: 22-3-2021
3616
التاريخ: 6-2-2016
1656
التاريخ: 20-4-2021
3088
التاريخ: 15-4-2021
1774
|
يمتاز هذا المنحني عن سواه من المنحنيات بأنه كلما ازدادت قيمة المتغير فيه تزداد التكرارات حتى يصل إلى نقطة معينة لا تعود بعدها قيمة المتغير إلى الانخفاض كما في الشكل :
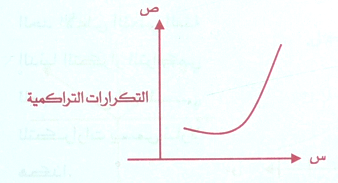
والمنحني الرائي المعكوس وكما في الشكل , وكلاهما يسمى منحني ذو شعبة واحدة .
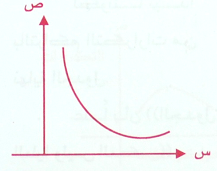
وأشهر مثال على المنحني الرائي المعكوس هو منحني توزيع ملكية الأراضي
في بعض البلدان حيث المساحات الصغيرة يمتلكها العدد الأكبر من السكان (التكرارات العليا) والمساحات الكبيرة يمتلكها العدد الأقل في السكان ( التكرارات الدنيا) .
|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
الأمانة العامة للعتبة الكاظمية المقدسة تستضيف مؤتمر أبناء الإمام الرضا الدولي الرابع
|
|
|
