


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 19-1-2019
Date: 4-3-2017
Date: 19-1-2019
|
The three-dimensional coordinate system is an extension of the twodimensional coordinate system invented in 1637 by French mathematician René Descartes (1596–1650). Soon after Descartes wrote about his twodimensional coordinate system, other mathematicians took Descartes’s idea and expanded it from a two-dimensional plane to three-dimensional space. This new development greatly enlarged the uses of the coordinate system.
With the enhancement of the two-dimensional coordinate system to three dimensions, it was possible to locate any object in three-dimensional space. For example, with Descartes’s two-dimensional coordinate system, you could describe the location of a coin on the floor of a room by referring to how many feet the coin was located from a front wall and a side wall.
However, in a two-dimensional coordinate system, it is impossible to describe the location of an object that is off the plane of the floor, such as the location of a crystal on a chandelier that is hanging from the ceiling. In a three-dimensional coordinate system, it is possible to refer to the location of a chandelier crystal with reference to the two walls of the room and also the floor.
Understanding Three-Dimensional Coordinates
A two-dimensional coordinate system is formed by two perpendicular lines designated as an x-axis and a y-axis. The two lines meet at a point called the origin. With a three-dimensional coordinate system, a third axis line is added. The third axis line intersects the other two axis lines at the origin, forming right angles with each of them. The x-axis shows locations of points in space lying in front and back of the origin. The y-axis shows the location of points in space to the left and to the right of the origin. The z-axis shows points in space lying above and below the origin.
One way to visualize a three-dimensional coordinate system is to imagine yourself standing in a room near one of its corners, and facing the corner. The x-axis extends along the base of the wall coming towards you. The y-axis extends along the base of the other wall (either extending to your left or right depending on which side of the corner you are facing). The z-axis extends upward to the ceiling.
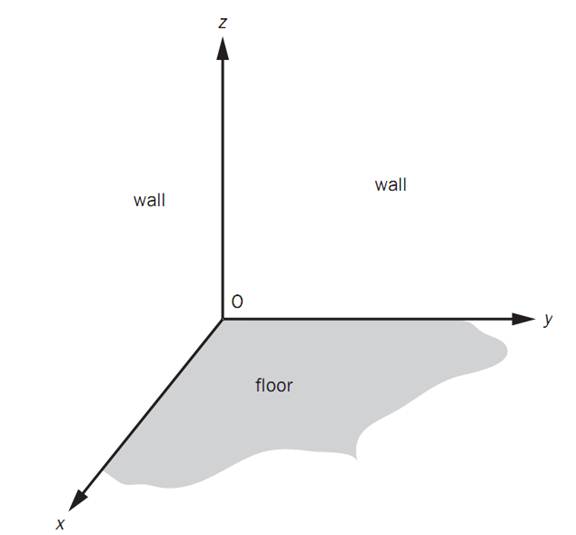
In the sketch above and its three-dimensional coordinate system shown below, suppose you are standing at point A. The coordinates of the soles of your feet would be (4, 3, 0), meaning that you are standing four units in front of the origin along the x-axis; three units to the right of the origin along the y-axis; and are neither above nor below the origin with respect to the z-axis. The coordinates of the top of your head might be (4, 3, 5), meaning that your head is 5 units above the origin. If your identical twin were standing in the next room directly “across” from you (through the wall) and at mirrored distances from both walls, the coordinates of his feet and head would be (4, 3, 0) and (4, 3, 5).
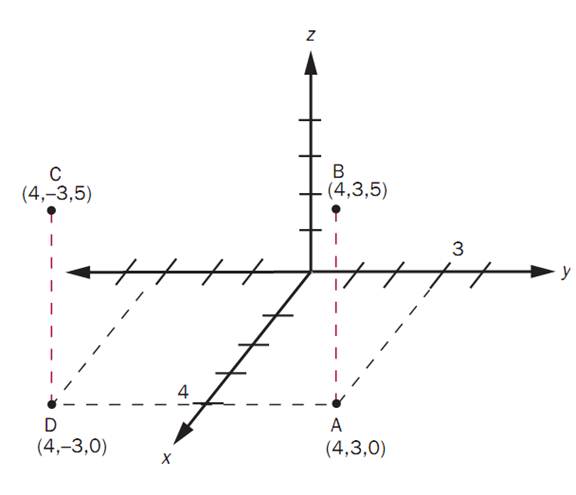
This diagram gives a limited illustration of how objects can be located using a three-dimensional coordinate system, because it shows only the four quadrants lying “toward” the observer or “in front of” the origin relative to the x-axis. There are four complementary quadrants lying “away from” the observer or “behind” the origin relative to the x-axis. Hence, the three -dimensional coordinate system can be used to represent any point in space relative to the three axis lines.
The three-dimensional coordinate system may also be used to determine the distance between any two points of a three-dimensional object. In the sketch above, the distance between Point B and the origin may be calculated by using the following formula:
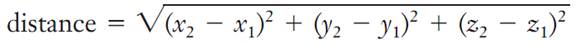
In this formula x1, y1, z1 represents the coordinates of Point B and x2, y2, z2 represents the coordinates of the origin. Thus the distance between PointB and the origin can be calculated as shown below.

______________________________________________________________________________________________
Reference
Bellman, Allan. Advanced Algebra: Tools for a Changing World. Needham, MA: Prentice Hall, 1998.
Clapham, Christopher. A Concise Oxford Dictionary of Mathematics. New York: Oxford University Press, 1990.



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|