
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
GAIN REVISITED
المؤلف:
Mark Csele
المصدر:
FUNDAMENTALS OF LIGHT SOURCES AND LASERS
الجزء والصفحة:
p143
14-3-2016
1718
GAIN REVISITED
We may now examine how gain relates to energy-level populations in the atomic system. We begin by expressing the gain coefficient of the system as proportional to the population inversion according to
g = (N2 - N1)σ0 (1.1)
where N2 - N1 is the population difference (ΔN) and σ0 is the cross section of the stimulated emission process. This states, not surprisingly, that gain is proportional to the population inversion as well as the cross section. Larger cross sections present more opportunity for stimulated emissions to occur and hence render larger gains. Cross section, as defined earlier, can be expressed mathematically as the product of the transition strength (or oscillator strength), S, and the line shape function of gain, g(v), which gives the normalized gain of the stimulated emission process at any given frequency. Graphically, transition strength is seen as the area under the curve, which defines the cross section as a function of frequency, as depicted in Figure 1.1.

Figure 1.1. Transition cross section and strength.
Transition strength is related to the spontaneous lifetime of the atomic species, so we may express cross section mathematically as
 (1.2)
(1.2)
where g(v) is the line shape of the gain function and tsp is the spontaneous lifetime of the species. So the cross section of the species is related to the spontaneous lifetime, an observable quantity in the laboratory. It may also be found in tables of physical constants for many species. This leaves the final term, called the line shape function for gain, to be defined.
Gain is actually a function of frequency (or wavelength, if you prefer). Since the laser transition is not infinitely sharp, it has a finite linewidth, so gain is spread out over a range (albeit a narrow range) of frequencies. The line shape of the gain function, for many lasers, is approximately Gaussian in shape, reaching a peak value of g(v0) at a center frequency v0 and tapering off at frequencies away from the center, as depicted in Figure 1.2. The gain can also be expressed as a function of wavelength (useful since line widths are often measured experimentally in terms of wavelength) as
 (1.3)
(1.3)

Figure 1.2. Typical gain line shape.
where δ is the FWHM width of the gain spectrum (in nm), which models, mathematically, the Gaussian shape of a typical gain curve. For many purposes it is sufficient to use a gain value at the maxima on the curve, at the center wavelength or frequency (denoted v0). A reasonable approximation for the gain curve is
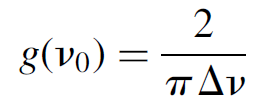 (1.4)
(1.4)
where Δv is the linewidth (FWHM) of the transition, which applies for most materials that feature what is called homogeneous broadening. For gases, which broaden with an inhomogeneous mechanism such as Doppler shifting, a better approximation is
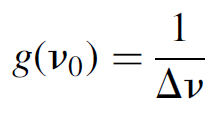 (1.5)
(1.5)
where Δv is the linewidth (FWHM) of the transition.
By substituting these approximations for the gain line shape into equation (1.2), we can calculate the maximum value of the cross section to yield σ(0) or s 0. Finally, using σ0 in equation (1.1), we may calculate the gain of the laser (or at least what is called the small-signal gain of the laser) for a given inversion. It is further possible to express the threshold gain of a laser in terms of the inversion required to obtain that gain by combining equation (1.1) with the equation for threshold gain. The threshold gain for an operating laser, and by equating the net gain to unity we yielded a simple equation to calculate threshold gain:
 (1.6)
(1.6)
We may simply combine this (multiplied by 2 to render an expression for round-trip loss in the laser) with equation (1.1) (by equating gth to g) to yield an answer for threshold in terms of the population inversion required to allow a laser to oscillate as follows:
 (1.7)
(1.7)
The numerator term in the equation represents round-trip losses, including absorption by the laser medium itself (2γl) as well as losses at both cavity mirrors [ln(1/R1R2)].
It is important to remember that as pump power to the laser is increased from zero, the inversion (ΔN) becomes progressively larger in proportion to pump power, as does laser gain. Since the gain is insufficient to overcome losses in the cavity, there is a net loss in the cavity and no laser action is observed. Eventually, pump power is sufficient to allow the inversion to reach the threshold value, at which point gain is equal to losses and laser action begins. At this point both gain and the amount of inversion are clamped at those threshold values, and a further increase in pump power to the laser does not increase gain but rather is manifested as an increase in laser output.
 الاكثر قراءة في مواضيع عامة في الليزر
الاكثر قراءة في مواضيع عامة في الليزر
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















