


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 2023-02-09
التاريخ: 2023-10-24
التاريخ: 24-7-2016
التاريخ: 26-4-2016
|
المتجه الرباعي
اي حدث مثل انبعاث اشارة ضوئية يمكن ان يوصف بموضعه (x, y, z) وبالزمن t حيث وقع الحدث. هذه المتغيرات الاربعة يمكن توحيدها بتعبير واحد أو علاقة منفردة تبقى دون تغيير فيما يخص تحويلات لورنس، اي انها لا تتغير بالنسبة لجميع محاور الاسناد. ان هذا النوع من التعبير يصبح مفيدا اذا ما اردنا معرفة كميات اخرى مماثلة في الميكانيك او في مواضيع الألكتروداينمك.
لترجع مرة اخرى الى تحويلات غاليليو فنلاحظ ان المسافة r2 بين نقطتين (x1,y1,z1) و (x2,y2,z2) تبقى دون تغيير بالنسبة لمحاور الاسناد اي ان :
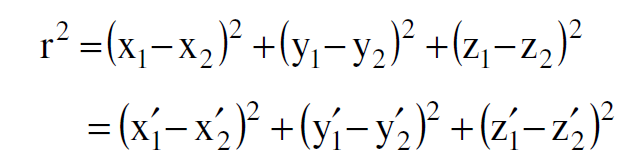
فاذا كانت النقطة (1) مثبتة في محور الاسناد s والنقطة (2) مثبتة في محور الاسناد sʹ تصبح r دالة للزمن، فنقول عندئذ ان r تبقى دون تغيير لان تحديدها يتم بدقة تحت التعبير نفسه في كلا محوري الاسناد. من الممكن ان نبين الان وبسهولة ان r لا تكون لها القيمة نفسها اي انها تتغير بالنسبة لتحويلات لورنس.
لنتصور وميضا ضوئيا انبعث من مصدر نقطي من نقطة الاصل o في اللحظة التي كانت فيها oʹ منطبقة على o. ان الضوء ينتقل من جميع الجهات وبسرعة c لكلا المحورين s و sʹ وعليه يكون :
 (1.1)
(1.1)
يصل الضوء الى النقطة (x, y, z) في زمن t ويصل الى النقطة (xʹ, yʹ, zʹ) في زمن tʹ فيكون لدينا :
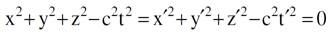
وبصورة عامة نرى ان الاحداثيات (x, y, z) و (xʹ, yʹ, zʹ) لأي حدث منفرد ترتبط مع بعضهما بعلاقة واحدة هي :

أو :
 (1.2)
(1.2)
فالكمية x2 + y2 + z2 – c2 t2 تبقى اذن دون تغيير تحت تحويلات لورنس. ان هذه الخاصية في الارتباط بين الاحداثيات الاربعة (x, y, z, t) تخضع بصورة مباشرة الى ه النوع من التحويلات.
وعليه فان اية مجموعة تتألف من اربع كميات تتحول بالطريقة نفسها التي تتحول بها الكميات (x, y, z, t) تظهر كمية مطابقة تبقى دون تغيير. ان مثل هذه الزمرة او المجموعة المكونة من كميات أربع يطلق عليها المتجه الرباعي.
قبل ان نبدأ بدراسة التمثيل الهندسي لتحويلات لورنس واستخدام المتجهات الرباعية علينا ان نعرف اولا ماذا يحدث لمتجه الموضع  ومقدارهr عندما تدور مجموعة من الاحداثيات (x, y, z) حول احداثي معين هو z بزاوية مقدارها θ لتتحول الى مجموعة اخرى من الاحداثيات ((xʹ, yʹ, zʹ
ومقدارهr عندما تدور مجموعة من الاحداثيات (x, y, z) حول احداثي معين هو z بزاوية مقدارها θ لتتحول الى مجموعة اخرى من الاحداثيات ((xʹ, yʹ, zʹ
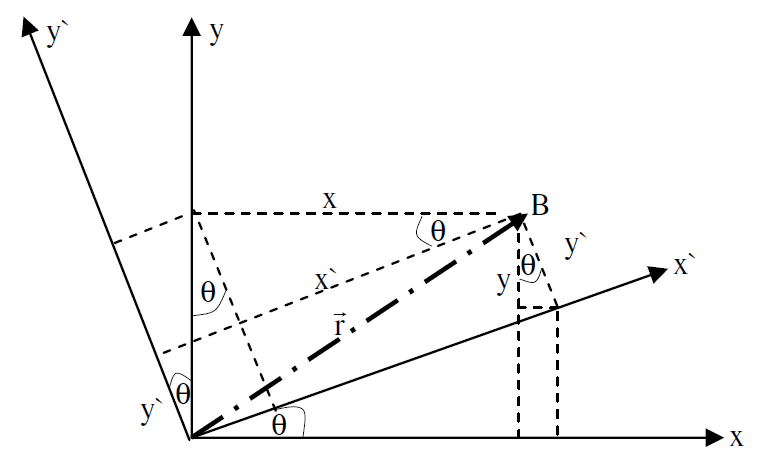
الشكل (1.1) : تحويل في ثلاثة ابعاد يسمى بالتحويل التعامدي، زاوية الدوران θ هي زاوية حقيقية.
ان تحويل الاحداثيات بواسطة هذا النوع من الدوران يوصف بالمعادلات الاتية، لاحظ الشكل (1.1):
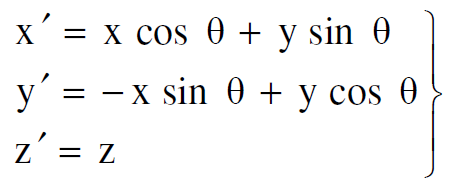 (1.3)
(1.3)
ان هذا التحويل الذي يبين عملية دوران الاحداثيات حول المحور z بزاوية θ حيث تحول الاحداثيات x, y يبقى مقدار المتجه 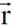 دون تغيير اذ من الممكن ان نحصل من المعادلات (1.3) على العلاقة الاتية :
دون تغيير اذ من الممكن ان نحصل من المعادلات (1.3) على العلاقة الاتية :
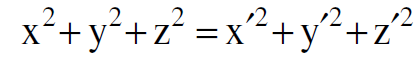
المعادلات (1.3) هي مثال لعملية تحويل في ثلاثة ابعاد يطلق عليه التحويل التعامدي. وهو تحويل حقيقي يترك مقدار المتجه 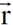 دون تغيير. ومن الممكن استخدام هذه الطريقة لتشمل ابعادا اربعة اذا اعتبرنا الكمية x2 + y2 + z2 – c2 t2 تمثل مربع بعد في احداثيات الفضاء والزمن. وعليه تعرف الاحداثيات الاربعة هذه كالاتي:
دون تغيير. ومن الممكن استخدام هذه الطريقة لتشمل ابعادا اربعة اذا اعتبرنا الكمية x2 + y2 + z2 – c2 t2 تمثل مربع بعد في احداثيات الفضاء والزمن. وعليه تعرف الاحداثيات الاربعة هذه كالاتي:
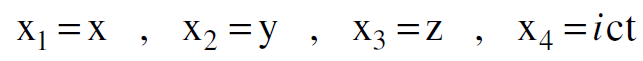
حيث ان  تكتب الكمية اذن على النحو الآتي :
تكتب الكمية اذن على النحو الآتي :
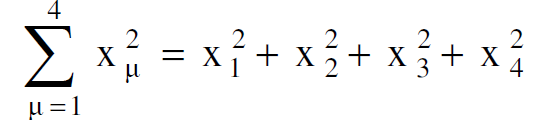 (1.4)
(1.4)
وهذه الكمية تبقى دون تغيير بالنسبة لتحويلات لورنس تحت شروط معينة. وتجدر الاشارة في هذا المجال الى ان الفضاء ذا الابعاد الاربعة يسمى كذلك فضاء "منكوسكي" نسبة الى العالم منكوسكي الذي أوجد مخططا لهذا الفضاء وقام بدراسته بصورة تفصيلية. في هذا الفضاء تعامل تحويلات لورنس على انها تحويل تعامدي والكمية المحددة بالإحداثيات x1,x2,x3,x4)) هي مركبات لمتجه رباعي في الفضاء ذي الابعاد الاربعة.



|
|
|
|
لشعر لامع وكثيف وصحي.. وصفة تكشف "سرا آسيويا" قديما
|
|
|
|
|
|
|
كيفية الحفاظ على فرامل السيارة لضمان الأمان المثالي
|
|
|
|
|
|
|
شعبة مدارس الكفيل: مخيَّم بنات العقيدة يعزِّز القيم الدينية وينمِّي مهارات اتخاذ القرار لدى المتطوِّعات
|
|
|