


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 24-7-2016
التاريخ: 24-4-2016
التاريخ: 25-9-2016
التاريخ: 24-4-2016
|
تغير الكتلة مع السرعة
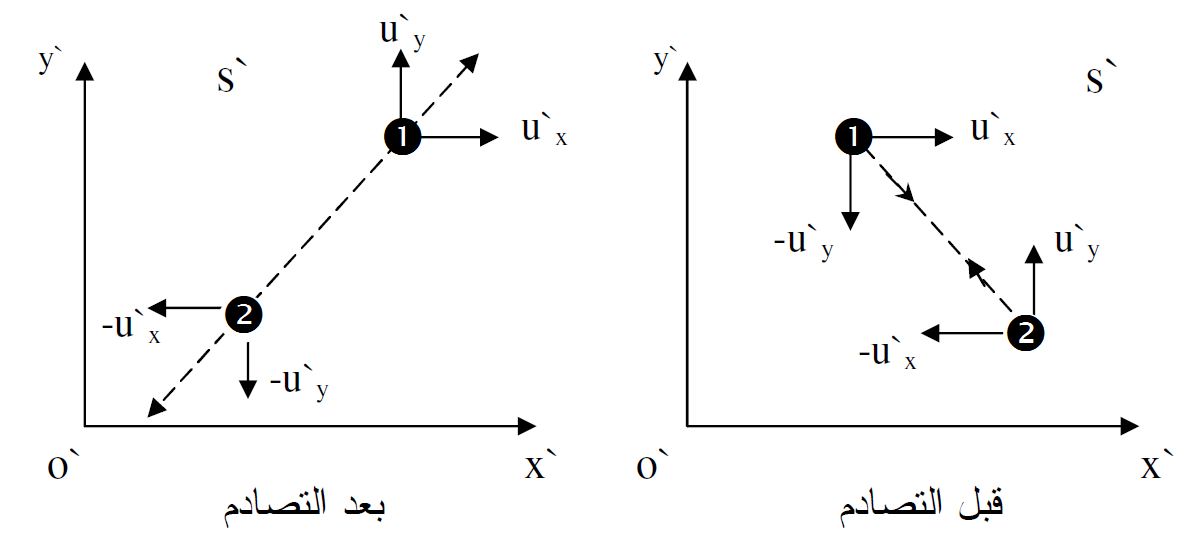
الشكل (1.1) محور الاسناد sʹ حيث تشاهد مركبات السرع لكرتين قبل وبعد التصادم بفرض ان التصادم مرن وتام.

الشكل (1.2) : محور الاسناد s حيث تشاهد مركبات السرع لكرتين قبل وبعد التصادم بفرض ان التصادم مرن وتام.
لابد لنا الآن أن ندرس المسالة الاساسية وهي كيفية تأثير تحويلات السرعة النسبية على قوانين الحركة لجسيم اذا ما اعتبرنا القوى والكتل.
لندرس تصادم جسمين متماثلين، ولنفرض ان التصادم تام المرونة بحيث يرتد الجسيمان دون تغيير في انطلاقهما النسبي. لنفرض ان مشاهدا في محور الاسناد .. يلاحظ الجسمين يقترب احدهما من الاخر على طول مسارين متوازيين بسرعتين متساويتين ومتعاكستين، كما في الشكل (1.1) قبل أن يحدث اي تصادم بينهما .
تحدث الحركة كليا في المستوى xʹ, yʹ وقد صنف الجسيمان برقمي 1 و2 ومركبتا سرعتيهما الابتدائيتان قبل التصادم بــ (uʹx,-uʹy) و uʹx) -uʹy,) على الترتيب. ويعاني كل من الجسيمين بعد التصادم انعكاسا في اتجاه مركبتي سرعتيهما باتجاه الاحداثي yʹ اما مركبتاهما باتجاه الاحداثي xʹ فتبقيان دون تغيير. اذن المركبتان النهائيتان لسرعة كل منهما بعد التصادم هما (uʹx, uʹy) و( (-uʹx,-uʹy كما هو موضح في الشكل (1.1).
لنصف الان نفس التصادم كما هو ملاحظ من قبل مشاهد في محور الاسناد s فتكون مركبتا سرعة الجسيم الاول قبل التصادم مساوية الى (u1x,-u1y) ومركبتا سرعة الجسيم الثاني (-u2x, u2y). وبعد التصادم يعاني كل من الجسيمين انعكاسا في اتجاه مركبتي سرعتيهما في اتجاه الاحداثي y كما هو ملاحظ في الشكل (1.2). فالقيم النهائية تكون اذن للجسيمين (u1x,u1y) و .(-u2x,-u2y)ووفقا لقواعد تحويلات السرعة نحصل على سرعة الجسيم الاول بعد التصادم :

وبالمثل نحصل على سرعة الجسيم الثاني بعد التصادم :
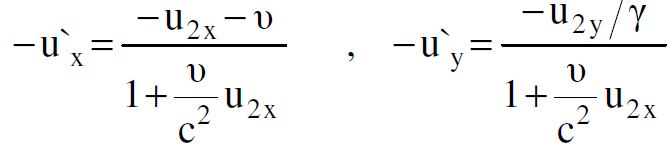
وعند حذف uʹx وuʹy من هذه العلاقات ينتج ان :
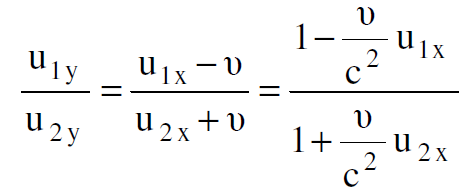
واذا حذفنا v من هذه المعادلات الاخيرة نحصل بعد اجراء بعض العمليات الجبرية، على العلاقة الاتية :
 (1.1)
(1.1)
حيث أن :
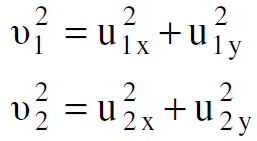
نستنتج من العلاقة الاخيرة ان u1y لا تساوي u2x كما هي مشاهد من قبل ملاحظ في محور الاسناد s بعد التصادم وذلك لاختلاف السرعتين 1v و2v.
اذن، اذا كانت كتلتا الجسيمين متساويتين، فالمركبتان u1y و u2x تعطيان زخمين غير متساويين، اي سوف لن يكون عندنا زخم خطي محفوظ. لذلك امامنا اختياران، اما ان ننبذ قانون حفظ الزخم الخطي او علينا ان نفرض ان كتلة الجسيم تعتمد بطريقة ما على حركة الجسيم بالنسبة لمشاهد معين. وبدلا من نبذ قانون الزخم الخطي اخترنا البديل الآخر.
نفرض الان ان كتلة الجسيم الاول الذي سرعته v1 كما هي مقاسة في محور الاسناد s مساوية الى m1 وللجسيم الثاني الذي سرعته v2 كما هي مقاسة في هذا المحور مساوية m2 نطبق قانون حفظ الزخم بالنسبة للجسيمين في محور الاسنادs فيكون باتجاه الاحداثي y :
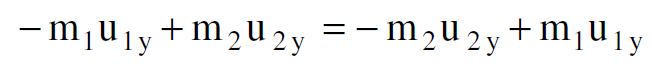
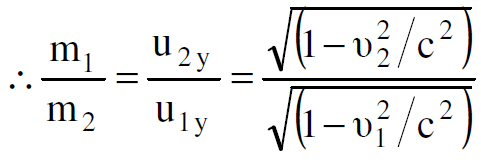 (1.2)
(1.2)
نفرض الان ان m1= m0 عندما تكون v2= 0 كتلة الجسيم عند السكون، وان m1= mعندما تكون v1=u كتلة الجسيم المتحرك بسرعة تساوي u.
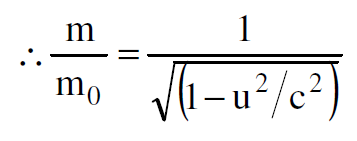
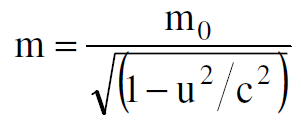 (1.3)
(1.3)
ومن الجدير بالذكر انه لو فرضنا ان كتلة الجسيم تبقى ثابتة حتى لو تغيرت سرعته، فان قانون حفظ الزخم لا يبقى محفوظا.
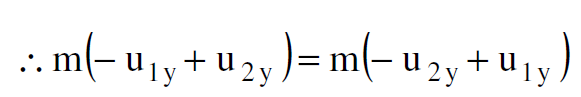
ومن هذا ينتج ان u1y= u2x وهذا يناقض العلاقة الاخيرة التي توصلنا اليها، وثبت فيها ان u1y≠ u2x. اذن لابد ان نعتبر ان الكل تتغير تبعا للسرعة وان قانون الزخم محفوظ.



|
|
|
|
لشعر لامع وكثيف وصحي.. وصفة تكشف "سرا آسيويا" قديما
|
|
|
|
|
|
|
كيفية الحفاظ على فرامل السيارة لضمان الأمان المثالي
|
|
|
|
|
|
|
شعبة مدارس الكفيل: مخيَّم بنات العقيدة يعزِّز القيم الدينية وينمِّي مهارات اتخاذ القرار لدى المتطوِّعات
|
|
|