


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 27-4-2016
التاريخ: 21-4-2016
التاريخ: 24-4-2016
التاريخ: 21-11-2020
|
نظرية التصادم غير المرن
في التصادم المرن تكون كل الطاقة حركية قبل وبعد التصادم، هذا اذا لم يؤخذ بالاعتبار طاقة الكتلة الساكنة. ومن المعروف في الميكانيك الاعتيادي لنيوتن ان الطاقة الحركية لا تبقى دائما محفوظة خلال التصادم، فأحيانا يحصل ان قسما من هذه الطاقة يتحول الى حرارة او صوت وفي أحيان اخرى قد تتحول الطاقة الحركية الى طاقة كامنة. يكون قانون حفظ الزخم قائما يمكن تطبيقه ضمن قوانين الميكانيك الاعتيادي لنيوتن ويمكن كذلك تطبيق قانون حفظ الطاقة اذا اخذت جميع صور الطاقة بنظر الاعتبار. ويمكن الان تطبيق قوانين حفظ الطاقة والزخم بصورة عامة في حالات التصادم التي تحدث بين الجسيمات عالية الطاقة حيث لا تكون الطاقة الحركية بالضرورة محفوظة. ولنأخذ الان مثالا يتعلق بالتصادم غير المرن بالكامل حيث تكون الطاقة الحركية في محور الاسناد sʹ مساوية صفرا بعد التصادم.
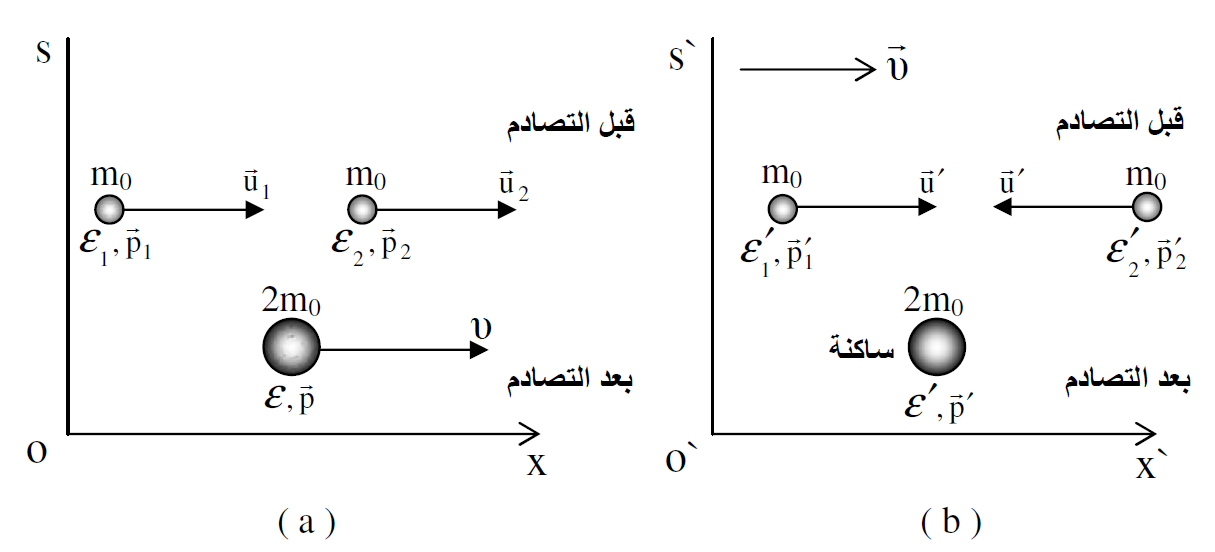
الشكل (1.1) : (a) عملية التصادم غير المرن بين جسيمين في s. b)) عملية التصادم غير المرن بين جسيمين فيsʹ .
لنعتبر كرتين الكتلة الساكنة لكل منهما m0 تتحرك احداهما بسرعة 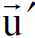 والاخرى
والاخرى  - باتجاه الاحداثي x الموجب في محور الاسناد sʹ ولنفرض حدوث تصادم غير مرن بالكامل بين هاتين الكرتين كما هو موضح في الشكل (1.1b) ولنعتبر ان الكرتين التصقتا مع بعضهما وكونتا كرة (كتلة) مشتركة بعد التصادم. وبما ان الزخم الكلي قبل التصادم يساوي صفرا في حالة بقاء الزخم محفوظا يحصل ان سرعة الكرة المشتركة بعد التصادم تساوي صفرا في محور الاسناد sʹ اما الطاقة الكلية للكرتين قبل التصادم في sʹ فهي تساوي :
- باتجاه الاحداثي x الموجب في محور الاسناد sʹ ولنفرض حدوث تصادم غير مرن بالكامل بين هاتين الكرتين كما هو موضح في الشكل (1.1b) ولنعتبر ان الكرتين التصقتا مع بعضهما وكونتا كرة (كتلة) مشتركة بعد التصادم. وبما ان الزخم الكلي قبل التصادم يساوي صفرا في حالة بقاء الزخم محفوظا يحصل ان سرعة الكرة المشتركة بعد التصادم تساوي صفرا في محور الاسناد sʹ اما الطاقة الكلية للكرتين قبل التصادم في sʹ فهي تساوي :
 (1.1)
(1.1)
حيث ان Tʹ مجموع الطاقتين الحركيتين للجسيمين قبل التصادم في محور الاسناد sʹ.
اذا فرض الان ان كل الطاقة الحركية في sʹ تتحول الى حرارة، تكون الحرارة المتولدة في هذا التصادم كما هي مقاسة في sʹ مساوية الى :
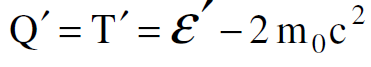 (1.2)
(1.2)
لنعتبر الان نفس هذا التصادم في محور الاسناد s حيث يتحرك بسرعة منتظمة -ῡ بالاتجاه الموجب للإحداثي x نسبة لمحور الاسناد sʹ كما هو ملاحظ في الشكل (1.1a). فالزخم الكلي للكرتين في s يمكن حسابه من معرفة الزخم الكلي والطاقة للكرتين في sʹ مباشرة قبل التصادم حيث تستعمل معادلات التحويل الخاصة بالزخم والطاقة بين محوري الاسناد، اي من sʹ الى s فيكون :
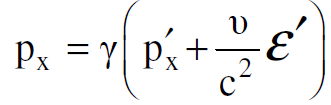
وبما أن الزخم الكلي يساوي صفرا في sʹ يحصل ان :

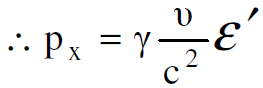 (1.3)
(1.3)
وبالاستعاضة عن قيمة ʹε المعطاة في المعادلة (1.2) يكون في حالة Qʹ=Tʹ ان :
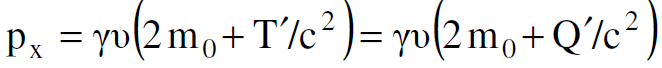 (1.4)
(1.4)
وبالمثل نكتب :

وبالمثل ايضا نجد ان الطاقة الكلية في s قبل التصادم يمكن حسابها باستخدام معادلات التحويل التالية :
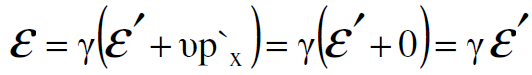
وبالاستعاضة عن ʹε في المعادلة (1.1) نحصل على الطاقة الكلية في s قبل التصادم وتساوي :
 (1.5)
(1.5)
يلاحظ بعد التصادم ان الكتلة المشتركة التي هي ساكنة في sʹ تتحرك بسرعة v في s. فاذا لم يحصل اي فناء للمادة خلال عملية التصادم نتوقع ان تكون الكتلة الساكنة للكرة المشتركة مساوية الى 2m0 ويصبح الزخم الكلي الخطي في s بعد التصادم مساويا الى :
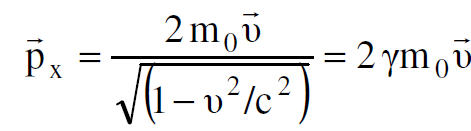 (1.6)
(1.6)
وبمقارنة هذه العلاقة الاخيرة مع العلاقة (1.4) نجد أنه لو كانت الكتلة الساكنة هي 2m0 لا يبقى الزخم محفوظا خلال التصادم. ولكي يبقى الزخم محفوظا في محور الاسناد s ينبغي ان نستبدل الكتلة 2m0 في العلاقة (1.6) بكتلة اخرى هي M0 حيث ان:
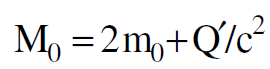 (1.7)
(1.7)
وعليه فان الزخم الخطي المساوي الى (v Qʹ/c2γ) قد ظهر نتيجة الحرارة التي تولدت خلال التصادم بفرض ان الزخم يبقى محفوظا في s. ان هذه الحرارة تتحرك مع الكتلة المشتركة بسرعة v في s ويكون زخمها مكافئا الى زخم الكتلة النسبية المساوية الى ( Qʹ/c2γ) في محور الاسناد s والكتلة النسبية المساوية الى Qʹ/c2 في محور الاسناد sʹ وهكذا تكون الطاقة الكلية للكتلة المشتركة في s بعد التصادم مساوية الى γM0 c2وترتبط مع Qʹ بالعلاقة التالية :
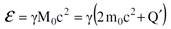 (1.8)
(1.8)
واذا قورنت المعادلتان (1.5) و (1.8) نجد أن الكلية تبقى محفوظة وذلك لان Tʹ = Qʹ في محور الاسناد sʹ.
نلاحظ مما تقدم انه اذا كان الزخم محفوظا في اي تصادم ينبغي على ضوء النظرية النسبية الخاصة ان يتم ارتباط كل من الكتلة القصرية* والزخم بجميع صور الطاقة بحيث لو فرض حصول اي تغيير في الطاقة مثل εΔ لرافقه تغير في الكتلة mΔ حيث أن :
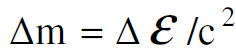
وان صحت هذه العلاقة لجميع صور الطاقة فانه عندما يحصل اي تغير في الطاقة لأي نظام، تتغير الكتلة القصرية لذلك النظام او بالعكس. من الممكن جعل هذه القاعدة عامة بحيث تطبق على الكتل الساكنة للجسيمات بعد ان يؤخذ بالاعتبار التكافؤ بين الكتلة والطاقة في جميع الحالات. وان كان هذا التكافؤ الوارد (أي بين الكتلة والطاقة) صحيحا من الناحية العلمية، فأنه يجب اثباته تجريبيا.
أول تجربة اجريت لأثبات العلاقة Δε= Δmc2 كانت في سنة 1932. حيث عجلت بروتونات حتى اصبحت طاقتها 0.25MeV بعدها تم توجيه هذه البروتونات المعجلة لقصف مادة الليثيوم كهدف فانبعث جسيما الفا باتجاهين متعاكسين. طاقة الجسيم الواحد 8.6MeV اذن الطاقة المكتسبة في هذا التفاعل تساوي :
2×8.6-0.25=16.95 MeV
حيث ان 0.25MeV هي الطاقة الحركية للبروتون الساقط. وكان نوع التفاعل هو :
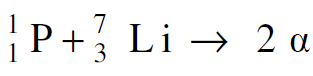
وباستخدام قيم الكتل الذرية يمكننا حساب الكمية mΔ :
(مجموع الكتل الناتجة عن التفاعل) – (مجموع الكتل الداخلة في التفاعل)= mΔ
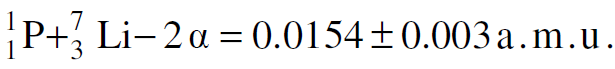
ان هذا الاختلاف في الكتلة يكافئ فرقا في الطاقة يساوي 14.3±2.7 MeV فاذا كانت العلاقة Δε= Δmc2 صحيحة. فان هذه النتيجة تتفق تماما مع الزيادة الحاصلة في الطاقة الحركية المساوية الى 16.95 MeV.
بالنسبة للطاقة التي تصل الى الارض من الشمس، من الممكن تقدير الطاقة الكلية المنبعثة من الشمس كما يلي :
إن كمية الطاقة المنبعثة من الشمس في الثانية تساوي : 4×1026 Js-1 وعيله يكون :
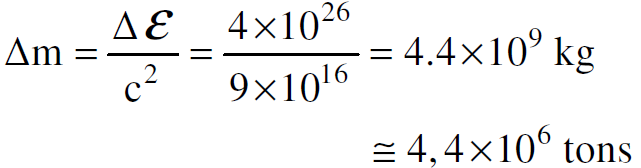
اي ان كتلة الشمس تتناقص بمعدل اربعة ملايين طن في كل ثانية. وهذه الكتلة صغيرة جدا مقارنة بكتلة الشمس التي تقدر بحوالي :
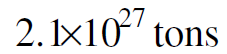
او

_____________________________________
*الكتلة القصرية (القصورية) هي نسبة الزخم الخطي الى السرعة ويقصد بها ايضا الكتلة النسبية و هي تتغير مع السرعة حسب العلاقة 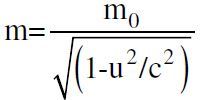 حيث ان m0 كتلة السكون.
حيث ان m0 كتلة السكون.



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
قسم الشؤون الفكرية يصدر كتاب الفلسفة الغربية برؤية الشيخ مرتضى مطهري
|
|
|