Is it true that the countries on any given map can be colored with four or fewer colors in such a way that adjacent countries are colored differently?

The seemingly simple Four Color Problem was introduced in 1852 by Francis Guthrie, a student of Augustus De Morgan. The first written reference to the problem is a letter from DeMorgan to Sir William Rowan Hamilton. Despite Hamilton’s indifference, De Morgan continued to talk about the problem with other mathematicians. In the years that followed, many of the world’s top mathematical minds attempted either to prove or disprove the conjecture, and in 1879 Alfred Kempe announced that he had found a proof. In 1890, however, P. J. Heawood discovered an error in Kempe’s proof. Kempe’s work did have some positive features, though, for Heawood made use of Kempe’s ideas to prove that five colors always suffice. In this section, we translate the Four Color Problem into a graph theory problem, and we prove the Five Color Theorem.

Any map can be represented by a planar graph in the following way: Represent each country on the map by a vertex, and connect two vertices with an edge whenever the corresponding countries share a nontrivial border (more than just a point). Some examples are shown in Figure 1.3.

                                 FIGURE 1.1. Graph representations of maps.

The regions on the map correspond to vertices on the graph, so a graph coloring yields a map coloring with no bordering regions colored the same. This natural representation allows us to see that a map is 4-colorable if and only if its associated graph is 4-colorable.

Theorem 1.1 (Four Color Theorem).

Every planar graph is 4-colorable.

When Heawood pointed out the error in Kempe’s proof, researchers flocked back to the drawing board. People worked on the Four Color Problem for years and years trying numerous strategies. Finally, in 1976, Kenneth Appel and Wolfgang Haken, with the help of John Koch, announced that they had found a proof .To complete their proof, they verified thousands of cases with computers, using over 1000 hours of computer time. As you might imagine, people were skeptical of this at first. Was this really a proof? How could an argument with so many cases be verified?

While the Appel–Haken proof is accepted as being valid, mathematicians still search for alternative proofs. Robertson, Sanders, Seymour, and Thomas [2]have probably come the closest to finding a short and clever proof, but theirs still requires a number of computer calculations.

In a 1998 article [3], Robin Thomas said the following.

For the purposes of this survey, let me telescope the difficulties with the A&H proof into two points: (1) part of the proof uses a computer and cannot be verified by hand, and (2) even the part that is supposedly hand-checkable has not, as far as I know, been independently verified in its entirety. ...Neil Robertson, Daniel P. Sanders, Paul Seymour, and I tried to verify the Appel–Haken proof, but soon gave up and decided that it would be more profitable to work out our own proof. ...We were not able to eliminate reason(1),but we managed to make progress toward (2).

As mentioned earlier, Heawood [4] provided a proof of the Five Color Theorem in the late 1890s, and we present his proof here. Some of the ideas in his proof came from Kempe’s attempt [5] to solve the Four Color Problem.

Theorem 1.3(Five Color Theorem). Every planar graph is 5-colorable.

Proof. We induct on the order of G. Let G be a planar graph of order n. If n ≤ 5, then the result is clear. So suppose that n ≥ 6 and that the result is true for all planar graphs of order n − 1. From [. If G is a planar graph, then G contains a vertex of degree at most five. That is, δ(G) ≤ 5.], we know that G contains a vertex, say v, having deg(v) ≤ 5.

Consider the graph G^/obtained by removing from G the vertex v and all edges incident with v. Since the order of G^/ is n − 1 (and since G^/is of course planar),  we can apply the induction hypothesis and conclude that G^/is 5-colorable. Now, we can assume that G^/ has been colored using the five colors, named 1, 2, 3, 4,  and 5. Consider now the neighbors of v in G. As noted earlier, v has at most five neighbors in G, and all of these neighbors are vertices in (the already colored) G^/.

If in G^/ fewer than five colors were used to color these neighbors, then we can properly color G by using the coloring for G^/ on all vertices other than v, and by coloring v with one of the colors that is not used on the neighbors of v. In doing this, we have produced a 5-coloring for G.

So, assume that in G^/ exactly five of the colors were used to color the neighbors of v. This implies that there are exactly five neighbors, call them w₁, w₂, w₃, w₄,  w₅, and assume without loss of generality that each wi is colored with color i (see Figure 1.1).

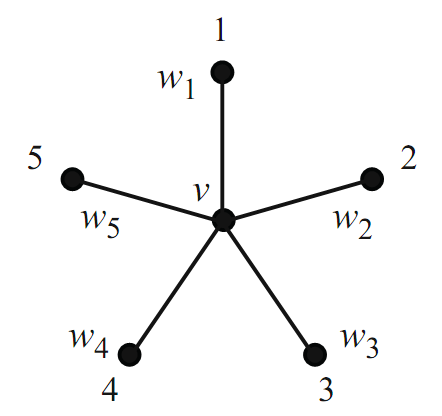
                               FIGURE 1.1.

We wish to rearrange the colors of G^/so that we make a color available for v. Consider all of the vertices of G^/ that have been colored with color 1 or with color 3.

Case 1. Suppose that in G^/ there does not exist a path from w₁ to w₃ where all of the colors on the path are 1 or 3. Define a subgraph H of G^/ to be the union of all paths that start at w₁ and that are colored with either 1 or 3. Note that w₃ is not avertex of H and that none of the neighbors of w₃ are in H (see Figure 1.2).

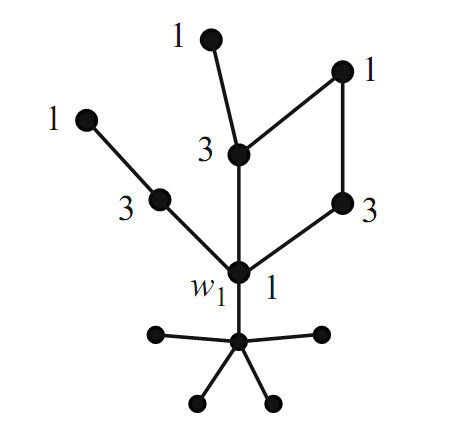
                                  FIGURE 1.2.

Now, interchange the colors in H. That is, change all of the 1’s into 3’s and all of the 3’s into 1’s. The resulting coloring of the vertices of G^/ is a proper coloring, because no problems could have possibly arisen in this inter change. We now see that w1 is colored 3, and thus color 1 is available to use for v. Thus, G is 5-colorable.

Case 2. Suppose that in G^/there does exist a path from w₁ to w₃ where all of the colors on the path are 1 or 3. Call this path P .Note now that P along with v forms a cycle that encloses either w₂ or w₄ (Figure 1.3).

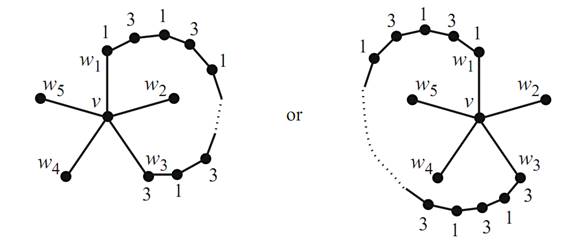
                                 FIGURE 1.3. Two possibilities.

So there does not exist a path from w2 to w4 where all of the colors on the path are 2 or 4. Thus, the reasoning in Case 1 applies! We conclude that G is 5-colorable.

________________________________________________________________________________________

1- Combinatorics and Graph Theory, Second Edition, John M. Harris • Jeffry L. Hirst • Michael J. Mossinghoff,2000,page(93-97)

2-N. Robertson, D. Sanders, P. Seymour, and R. Thomas, The four-colour theorem, J. Combin.Theory Ser. B 70 (1997), no. 1, 2–44.

3-R. Thomas, An update on the four-color theorem, Notices Amer. Math. Soc. 45 (1998), no. 7,848–859.

4-P. J. Heawood, Map-colour theorem, Quart. J. Math. 24 (1890), 332–339.

5-A. B. Kempe, On the geographical problem of the four colors,Amer.J.Math. 2 (1879), no. 3,193–200.

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم بين الحرمين يقدم ورشة تدريبية عن صيانة العجلات الكهربائية للملاكات الفنية في مدينة الفردوس

مجموعة مشاتل الكفيل تستقبل طلبة مجموعة العميد التربوية

قسم العلاقات العامة ينظم محاضرة ثقافية لوفد مركز الزهراء (عليها السلام) من ألمانيا

المجمع العلمي يحيي ذكرى ولادة الإمام علي (عليه السلام) في كربلاء

المزيد

الآخبار الصحية

طبيب يكشف أفضل مكمل غذائي لتحسين المزاج ودعم الصحة النفسية

دراسة جديدة تكشف أضرار الأطعمة الجاهزة على القلب ؟

6 أطعمة طبيعية تهدئ الزكام دون أدوية.. تعرف عليهم

ماذا يحدث لأعراض الزكام عند تناول الثوم بانتظام؟

المزيد

الآخبار التكنلوجية

ابتكار ثوري في بطاريات السيارات الكهربائية.. سعة أعلى 4 مرات

ماذا يحدث لجسمك عند شرب الماء الساخن يوميا؟

7 فوائد "خفية" لشرب شاي الكركديه كل يوم

دراسة تكشف قدرة الحيتان على سماع الأصوات منخفضة وعالية التردد من مسافة بعيدة

المزيد

مواضيع ذات صلة

Minimum Spanning Tree

Maximum Leaf Number

Lobster Graph

Labeled Tree

Internal Path Length

Red-Black Tree

Pseudotree

Pseudoforest

Prüfer Code

Planted Tree

Planted Planar Tree

Graph Strength