


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 18-8-2016
Date: 3-9-2016
Date: 11-8-2016
|
Maxwell-Boltzmann Averages
a) Write the properly normalized Maxwell–Boltzmann distribution f (v) for finding particles of mass m with magnitude of velocity in the interval [v, v + dv] at a temperature τ.
b) What is the most likely speed at temperature τ.
c) What is the average speed?
d) What is the average square speed?
SOLUTION
a) We may write the unnormalized Maxwell–Boltzmann distribution immediately as
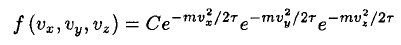 (1)
(1)
We would like to write (1) as f (v) so we must integrate over all velocities in order to find the proper normalization:
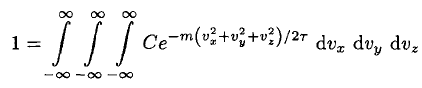 (2)
(2)
Rewriting (2) in spherical coordinates v, θ, φ, we have
 (3)
(3)
A variety of problems contain the definite integral (3) and its variations. A particularly easy way to derive it is to start by writing the integral as
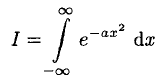 (4)
(4)
Now multiply I by itself, replacing x by y yielding
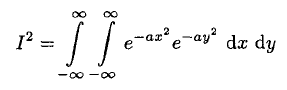 (5)
(5)
Rewriting (5) in polar coordinates gives
 (6)
(6)
where we have substituted v = au2 in (6). So we have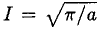 Integrating instead from 0 to ∞ then gives
Integrating instead from 0 to ∞ then gives
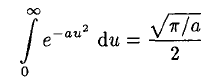 (7)
(7)
The integral required here may be found by differentiating (7) once with respect to a:
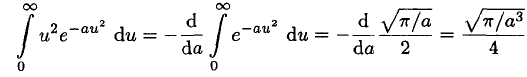 (8)
(8)
Using (8) in (3), where a = m/2τ, gives
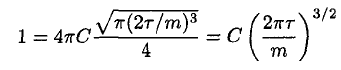 (9)
(9)
so
 (10)
(10)
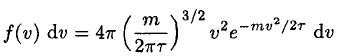 (11)
(11)
b) The most likely speed u occurs when (11) is a maximum. This may be found by setting its derivative or, simply the derivative of In f (v), equal to 0:
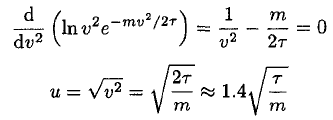 (12)
(12)
c) The average speed is given by
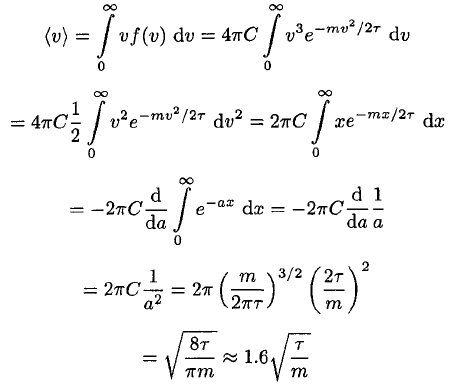 (13)
(13)
d) The mean square speed of the atoms may be found immediately by recalling the equipartition theorem and using the fact that there is τ/2 energy per degree of freedom. So
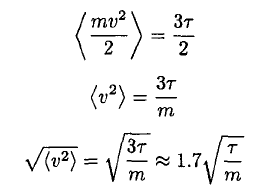 (14)
(14)
For completeness, though, the integral may be shown:
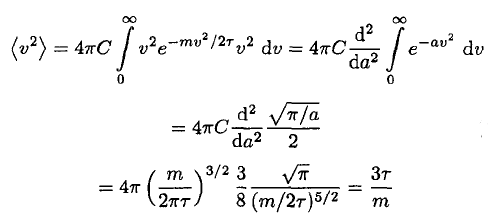 (15)
(15)



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|