


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات | Differentiation and Integration in RN-Taylor,s Theorem; Maxima and Minima |
|
|
|
Read More
Date: 22-11-2016
Date: 24-11-2016
Date: 23-11-2016
|
Definitions
Let f be a function from RN into R1.We define the second partial derivative f,i,j asthe first partial derivative of f,i with respect to xj . We define the third partial derivative f,i,j,k as the first partial derivative of f,i,j . Fourth, fifth, and higher derivatives are defined similarly. In computing second partial derivatives it is natural to ask whether the order of computation affects the result. That is, is it always true that f,i,j = f,j,i for i ≠j? There are simple examples that show that the order of computation may lead to different results. (See Problem 3 at the end of this section.) The next theorem, stated without proof, gives a sufficient condition that validates the interchange of order of partial differentiation.
Theorem 1.1
Let f :RN → R1 be given and suppose that f , f,i , f,i,j , and f,j,i are all continuous at a point a. Then
f,i,j (a)= f,j,i(a).
Definitions
A multi-index α is an element (α1,α2,...,αN) in RN where each αi is a nonnegative integer. The order of a multi-index, denoted by |α|,is the nonnegative integer α1 +α2 +...+αN. We extend the factorial symbol to multi-indices by defining α! =α1! · α2! ··· αN!. If β is another multi-index (β1,β2,...,βN), we define
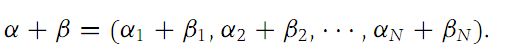
Let x =(x1,x2,...,xN) be any element of RN. Then the monomial xα is defined by the formula
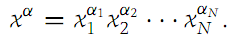
Clearly, the degree of xα is |α|. Any polynomial in RN is a function f of the form (1.1)
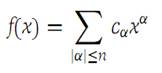
in which α is a multi-index, the cα are constants, and the sum is taken over all multi-indices with order less than or equal to n, the degree of the polynomial.
Lemma 1.1 (Binomial theorem)
Suppose that x, y ∈ R1 and n is a positive integer. Then
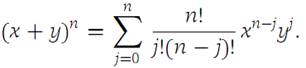
The proof is easily established by induction on n, and we leave the details to the reader. The Multinomial theorem, an extension to several variables of the binomial theorem, is essential for the development of the Taylor expansion for functions of several variables. We state the result without proof, although the formula is not difficult to establish by induction. (Fix the integer n and use induction on N.)
Lemma 1.2 (Multinomial theorem)
Suppose that x= (x1,x2,...,xN) is an element of RN and that n is any positive integer. Then
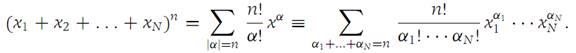
Let G be an open set in RN and let f : G → R1 be a function with continuous second derivatives in G. We know that in the computation of second derivatives the order of differentiation may be interchanged. That is, f,i,j = f,j,i for all i and j. We may also write f,i,j = Dj [Di f ]. With any polynomial in RN of the form(1.2)
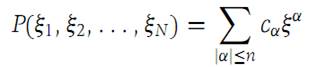
we associate the operator(1.3)

If α is the multi-index (α1,α2,...,αN), then Dα is the operator given by Dα =Dα11 Dα22 ··· DαNN . That is, Dαf means that f is first differentiated with respect to xN exactly αN times; then it is differentiated αN−1 times with respect to xN−1, and so on until all differentiations of f are completed.
The order of the operator (1. 3) is the degree of the polynomial (1. 2). By induction it is easy to see that every operator consisting of a linear combination of maps is of the form (1. 3). The differentiations may be performed in any order. The polynomial P(ξ1,ξ2,...,ξN) in (1. 2) is called the auxiliary polynomial of the operator (1. 3).
Definitions
Let f : RN → R1 be a given function, and suppose that a ∈ RN and b ∈ RN with |b|= 1. The directional derivative of f in the direction p at the point , denoted by db f(a), is the number defined by(1.4)
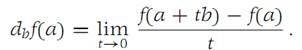
Note that the difference quotient in the definition is taken by subtracting f(a) from the value of f taken on the line segment in RN joining a and a + b. The second directional derivative of f in the direction b at the point a is simply db[dbf ](a), and it is denoted b (db)2f(a). The nth directional derivative, (db)nf(a), is defined similarly.
Lemma 1.3
Suppose that f :RN → R1 and all its partial derivatives up to and including order n are continuous in a ball B(a,r). Then(1.5)
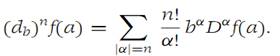
Symbolically, the nth directional derivative is written
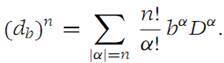
Proof
For n = 1, we set φ(t) = f(a + tb). Then dbf(a)= φ/(0). We use the Chain rule to compute φ/, and denoting b = (b1,b2,...,bN),we find
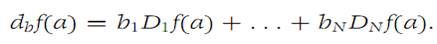
That is, db= b1D1 + ... + bND=. By induction, we obtain
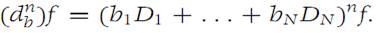
Using the Multinomial theorem(Lemma 1.2),we get equation (1. 5).
Theorem 1.2(Taylor’s theorem for functions from R1 to R1)
Suppose that f :R1 to R1 and all derivatives of f up to and including order n+1 are continuous on an interval I ={x:|x − a| <r}. Then for each x on I, there is a number ξ in the open interval between a and x such that(1.6)
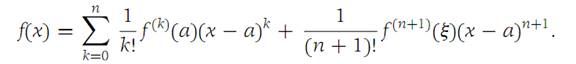
The proof of Theorem1.2makesuse of Rolle’s theorem and is deferred. formula (1. 6) is the Mean-value theorem. (See Problem 3 at the end of this section and the hint given there.) The last term in (1. 6) is called the remainder.
We now use Theorem1.2to establish Taylor’s theorem for functions from a domain in RN to R1.
Theorem1.3 (Taylor’s theorem with remainder)
Suppose that f :RN → R1 and all its partial derivatives up to and including order n + 1 are continuous on a ball B(a,r). Then for each x in B(a,r), there is a point ξ on the straight line segment from a to x such that(1.7)
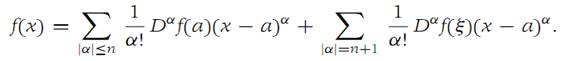
Proof
If x =a, the result is obvious. If x ≠a, define b =(b1 ,b 2,...,bN ) by
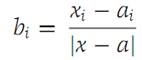
We note that |b|=1 and define φ(t) = f(a + tb). We observe that φ(0) = f(a) and φ(|x − a|) = f(a +|x − a|· b) = f(x). By induction, it follows that φ has continuous derivatives up to and including order n + 1, since f does. Now we apply Taylor’s theorem (Theorem 1.2) to φ, a function of one variable. Then(1.8)
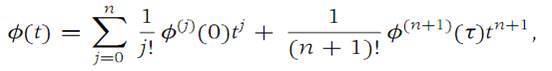
where τ is between 0 and t. From Lemma 1.3, the formula for (db)j ,it follows that)1.9)

We set t =|x − a| in equation (1. 8), getting

Inserting equation (1. 9) into this expression, we find
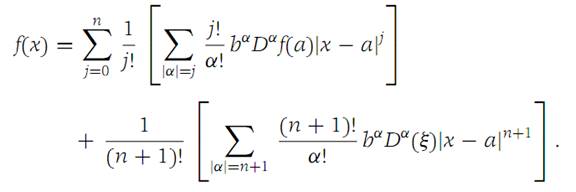
By definition we have xi − ai =bi |x − a|, and so (x − a)α = bα|x − a| |α|.
Employing this fact in the above expression for f(x), we obtain equation (1. 7).
The last terms in formula (1. 7) are known as the remainder. For functions from R1 into R1 the second derivative test is one of the most useful for identifying the maximum and minimum points on the graph of the function. We recall that a function f with two derivatives and with f/(a) = 0 has a relative maximum at a if its second derivative at a Is negative. It has a relative minimum at a if f//(a) > 0. If f// (a) = 0, the test fails. With the aid of Taylor’s theorem for functions from RN into R1 we can establish the corresponding result for functions of N variables.
Definitions
Let f : RN → R1 be given. The function f has a local maximum at the value a if there is a ball B(a, r) such that f(x) − f(a) ≤ 0 for x ∈ B(a, r). The function f has a strict local maximum at a if f(x) − f(a) < 0 for x ∈ B(a, r) except for x = a. The corresponding definitions for local minimum and strict local minimum reverse the inequality sign. If f has partial derivatives at a, we say that f has a critical point at the value a if Di f(a) = 0, i =1, 2,...,N.
Theorem 1.4 (Second derivative test)
Suppose that f :RN → R1 and its partial derivatives up to and including order 2 are continuous in a ball B(a, r). Suppose that f has a critical point at a. For
h = (h1,h2,...,hN), define Δf (a,h) = f(a + h) − f(a); also define (1.10)
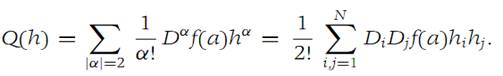
(a) If Q(h)> 0 for h≠ 0, then f has a strict local minimum at a.
(b) If Q(h)< 0 for h ≠ 0, then f has a strict local maximum at a.
(c) IfQ(h) has a positive maximum and a negative minimum, thenΔf (a,h) changes sign in any ball B(a,ρ) such that ρ<r.
Proof
We establish part (a), the proofs of parts (b) and (c) being similar. Taylor’s theorem with remainder (Theorem 1.3) for n = 1 and x = a + h is(1.11)
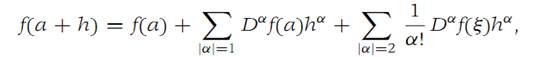
where ξ is on the straight line segment connecting a with a + h. Since f has a critical point at a, the first sum in Equation (1.11) is zero, and the second sum may be written (1.12)
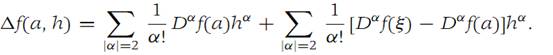
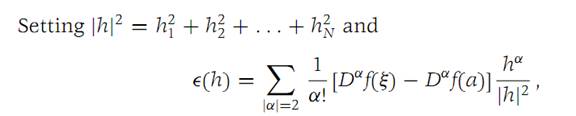
we find from equation (1.12) that(1.13)

Because the second partial derivatives of f are continuous near a,it follows that Ԑ(h) → 0as h → 0. Also,
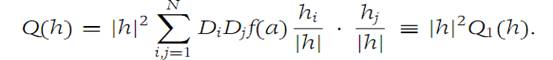
The expression Q1(h) is continuous for h on the unit sphere in RN. According to the hypothesis in part (a), Q1, a continuous function, must have a positive minimum on the unit sphere, which is a closed set. Denote this minimum by m. Hence,
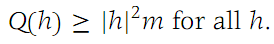
Now choose |h| so small that |Ԑ(h)| <m/2. Inserting the inequalities for Q(h) and |Ԑ(h)| into equation (1.13),we find

for |h| sufficiently small and h =0. We conclude that f has a strict local minimum at a.
Problems
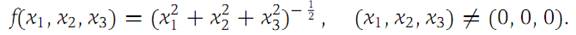
Show that f satisfies the equation
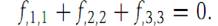
2.Given f : R2 → R1 defined by
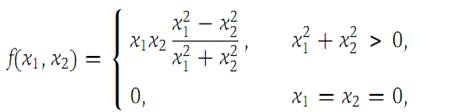
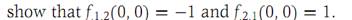
3. Find the relative maxima and minima of the function f : R2 → R1 given by
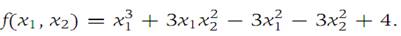
Basic Elements of Real Analysis, Murray H. Protter, Springer, 1998 .Page(129-136)



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|