
Quantitative treatment of hole burning. Single mode laser action of an inhomogeneously broadened line
 المؤلف:
H. HAKEN
المؤلف:
H. HAKEN
 المصدر:
LASER LIGHT DYNAMICS
المصدر:
LASER LIGHT DYNAMICS
 الجزء والصفحة:
vol 2 ، p85
الجزء والصفحة:
vol 2 ، p85
 26-12-2016
26-12-2016
 1968
1968
Quantitative treatment of hole burning. Single mode laser action of an inhomogeneously broadened line
We now return to single mode laser action in a solid state laser with an inhomogeneously broadened line. We start from the mode which we write down for the special case of a single mode where we drop the index A of n but retain it for sake of clarity in Wλμ. Neglecting as usual spontaneous emission this equation reads
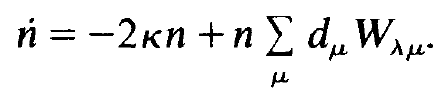 (1.1)
(1.1)
We insert in it the saturated inversion reads
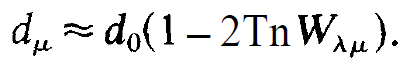 (1.2)
(1.2)
We adopt running waves so that Wλμ does no more depend on the space coordinate x. Using the explicit form of Wλμ as and replacing the index μ by I we may write
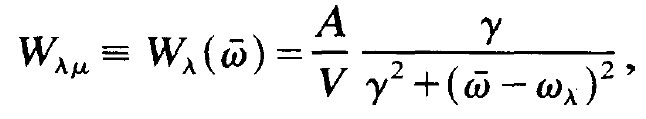 (1.3)
(1.3)
where we have used the abbreviation
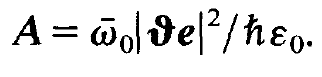 (1.4)
(1.4)
By inserting (1.2) into (1.1) we cast eq. (1.1) into the form
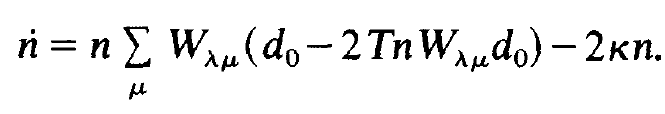 (1.5)
(1.5)
We convert the sum over the atomic indices μ into an integral over space and an integral over the frequencies 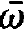 ,
,
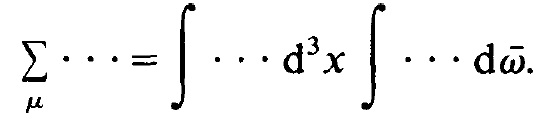 (1.6)
(1.6)
Because W does not depend on space the integration over the volume elements d3x yields the volume V of the resonator. In order to evaluate the integral over I we use a Gaussian distribution for the frequency distribution
ρ(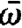 ), i.e.
), i.e.
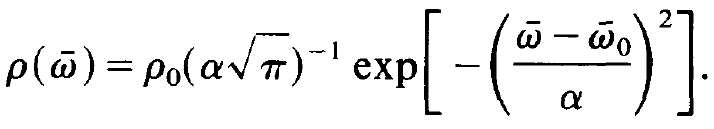 (1.7)
(1.7)
Here ρ0 is the density of atoms, ρ0 = N/ V, where N is the total number of laser atoms in the resonator and V the volume of the resonator, and a is the half width of the Gaussian distribution. We first treat the first term on the r.h.s. of (1.5),
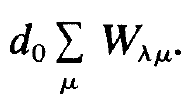 (1.8)
(1.8)
In order to evaluate this expression we insert (1.3) and (1.7) into it. Observing that integration over the volume in (1.6) cancels against V in the denominator in (1.3) we have eventually to treat
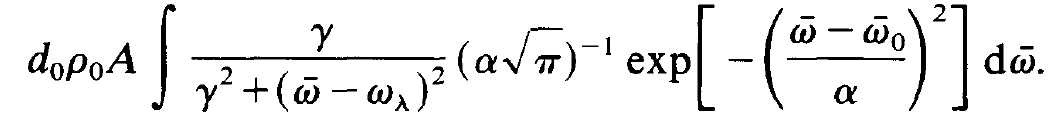 (1.9)
(1.9)
This integral cannot be evaluated in explicit form. However, it is rather simple to calculate it approximately if we assume y << a. In such a case we obtain in a good approximation
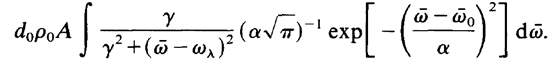
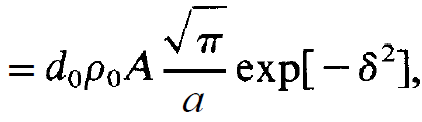 (1.10)
(1.10)
where δ is defined by
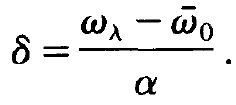 (1.11)
(1.11)
In a similar fashion we can evaluate the second term in (1.5), i.e.
 (1.12)
(1.12)
which yields
 (1.13)
(1.13)
Taking the corresponding terms together, we may cast (1.5) into the explicit form
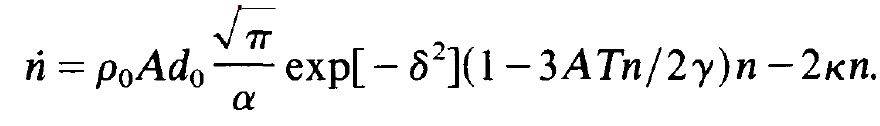 (1.14)
(1.14)
the stationary state, dn/dt = 0, this equation can be readily solved for n. Because n is the only free parameter in the formula for hole burning, (1.2), we have thus fixed the depth of that hole. We mention that the integrals such as (1.9) can be evaluated exactly and explicitly if the inhomogeneous atomic line is a Lorentzian.
 الاكثر قراءة في مواضيع عامة في الليزر
الاكثر قراءة في مواضيع عامة في الليزر
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


