
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء والفلسفة

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Complex numbers
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المصدر:
The Feynman Lectures on Physics
الجزء والصفحة:
Volume I, Chapter 22
2024-03-10
2057
Now it turns out that after all that work, we still cannot solve every equation! For instance, what is the square root of −1? Suppose we have to find x2=−1. The square of no rational, of no irrational, of nothing that we have discovered so far, is equal to −1. So we again have to generalize our numbers to a still wider class. Let us suppose that a specific solution of x2=−1 is called something, we shall call it i; i has the property, by definition, that its square is −1. That is about all we are going to say about it; of course, there is more than one root of the equation x2=−1. Someone could write i, but another could say, “No, I prefer −i. My i is minus your i.” It is just as good a solution, and since the only definition that i has is that i2=−1, it must be true that any equation we can write is equally true if the sign of i is changed everywhere. This is called taking the complex conjugate. Now we are going to make up numbers by adding successive i’s, and multiplying i’s by numbers, and adding other numbers, and so on, according to all of our rules. In this way we find that numbers can all be written in the form p+iq, where p and q are what we call real numbers, i.e., the numbers we have been defining up until now. The number i is called the unit imaginary number. Any real multiple of i is called pure imaginary. The most general number, a, is of the form p+iq and is called a complex number. Things do not get any worse if, for instance, we multiply two such numbers, let us say (r+is)(p+iq). Then, using the rules, we get
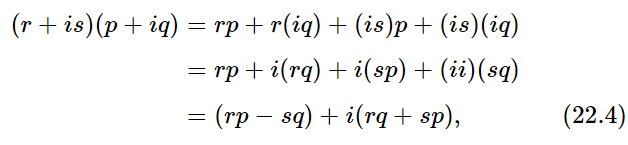
since ii= i2= −1. Therefore all the numbers that now belong in the rules (22.1) have this mathematical form.
Now you say, “This can go on forever! We have defined powers of imaginaries and all the rest, and when we are all finished, somebody else will come along with another equation which cannot be solved, like x6+3x2=−2. Then we have to generalize all over again!” But it turns out that with this one more invention, just the square root of −1, every algebraic equation can be solved! This is a fantastic fact, which we must leave to the Mathematics Department to prove. The proofs are very beautiful and very interesting, but certainly not self-evident. In fact, the most obvious supposition is that we are going to have to invent again and again and again. But the greatest miracle of all is that we do not. This is the last invention. After this invention of complex numbers, we find that the rules still work with complex numbers, and we are finished inventing new things. We can find the complex power of any complex number, we can solve any equation that is written algebraically, in terms of a finite number of those symbols. We do not find any new numbers. The square root of i, for instance, has a definite result, it is not something new; and ii is something. We will discuss that now.
We have already discussed multiplication, and addition is also easy; if we add two complex numbers, (p+iq)+(r+is), the answer is (p+r)+i(q+s). Now we can add and multiply complex numbers. But the real problem, of course, is to compute complex powers of complex numbers. It turns out that the problem is actually no more difficult than computing complex powers of real numbers. So let us concentrate now on the problem of calculating 10 to a complex power, not just an irrational power, but 10(r+is). Of course, we must at all times use our rules (22.1) and (22.2). Thus

But 10r we already know how to compute, and we can always multiply anything by anything else; therefore, the problem is to compute only 10is. Let us call it some complex number, x+iy. Problem: given s, find x, find y. Now if
10is = x + iy,
then the complex conjugate of this equation must also be true, so that
10−is = x − iy.
(Thus we see that we can deduce a number of things without actually computing anything, by using our rules.) We deduce another interesting thing by multiplying these together:
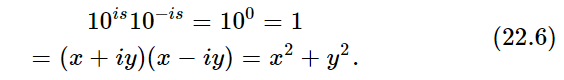
Thus, if we find x, we have y also.
Now the problem is how to compute 10 to an imaginary power. What guide is there? We may work over our rules until we can go no further, but here is a reasonable guide: if we can compute it for any particular s, we can get it for all the rest. If we know 10is for any one s and then we want it for twice that s, we can square the number, and so on. But how can we find 10is for even one special value of s? To do so we shall make one additional assumption, which is not quite in the category of all the other rules, but which leads to reasonable results and permits us to make progress: when the power is small, we shall suppose that the “law” 10ϵ=1+2.3025ϵ is right, as ϵ gets very small, not only for real ϵ, but for complex ϵ as well. Therefore, we begin with the supposition that this law is true in general, and that tells us that 10is=1+2.3025⋅is, for s→0. So we assume that if s is very small, say one part in 1024, we have a rather good approximation to 10is.
Now we make a table by which we can compute all the imaginary powers of 10, that is, compute x and y. It is done as follows. The first power we start with is the 1/1024 power, which we presume is very nearly 1+2.3025i/1024. Thus we start with
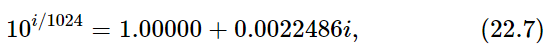
and if we keep multiplying the number by itself, we can get to a higher imaginary power. In fact, we may just reverse the procedure we used in making our logarithm table, and calculate the square, 4th power, 8th power, etc., of (22.7), and thus build up the values shown in Table 22–3. We notice an interesting thing, that the x numbers are positive at first, but then swing negative. We shall look into that a little bit more in a moment. But first we may be curious to find for what number s the real part of 10is is zero. The y-value would be 1, and so we would have 10is=1i, or is=log10 i. As an example of how to use this table, just as we calculated log10 2 before, let us now use Table 22–3 to find log10 i.
Table 22–3
Successive Squares of 10i/1024=1+0.0022486i

Which of the numbers in Table 22–3 do we have to multiply together to get a pure imaginary result? After a little trial and error, we discover that to reduce x the most, it is best to multiply “512” by “128.” This gives 0.13056+0.99159i. Then we discover that we should multiply this by a number whose imaginary part is about equal to the size of the real part we are trying to remove. Thus, we choose “64” whose y-value is 0.14349, since that is closest to 0.13056. This then gives −0.01308+1.00008i. Now we have overshot, and must divide by 0.99996+0.00900i. How do we do that? By changing the sign of i and multiplying by 0.99996−0.00900i (which works if x2+y2=1). Continuing in this way, we find that the entire power to which 10 must be raised to give i is i(512+128+64−4−2+0.20)/1024, or 698.20i/1024. If we raise 10 to that power, we can get i. Therefore, log10 i=0.68184i.
 الاكثر قراءة في الفيزياء الرياضية
الاكثر قراءة في الفيزياء الرياضية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















