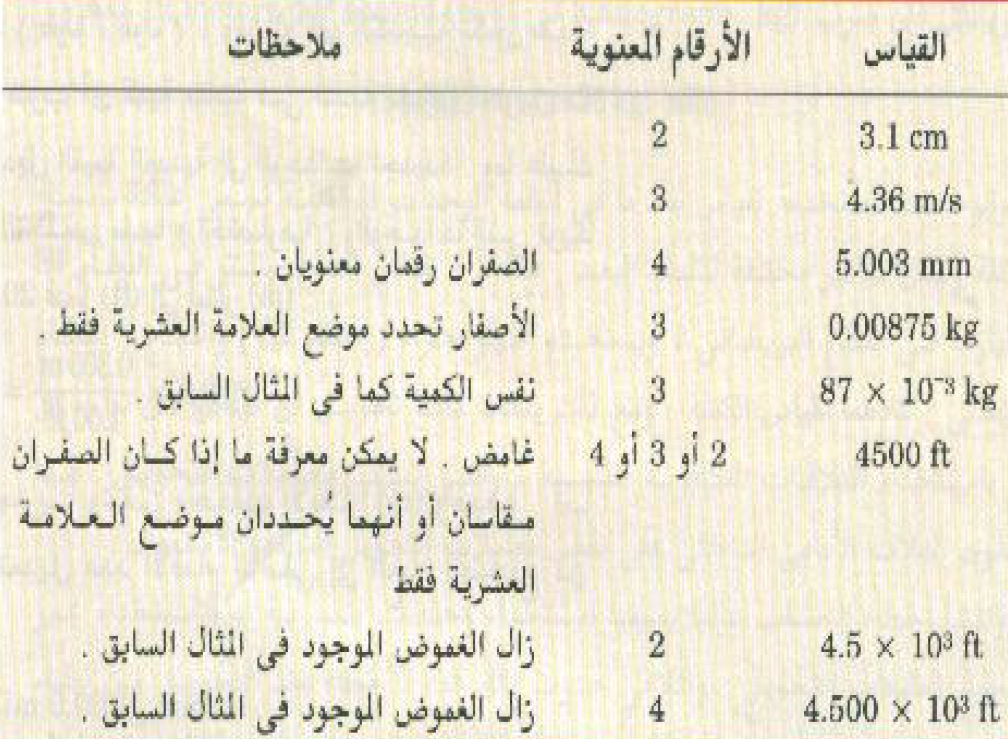
من الضروري عند إجراء الحسابات معرفة عدد الأرقام المعنوية اللازم الاحتفاظ بها في النتيجة. ذلك أن الآلات الحاسبة تعطي النتيجة على هيئة عدد مكون مما يقرب من عشرة أرقام حتى وإن كانت الكميات المدخلة مكونة من عددية معنويين أو ثلاثة فقط. وسوف نتعرف خلال هذا المقرر على قاعدتين بسيطتين لحل هذه المشكلة.
الارقام المعنوية في عمليتي الجمع او الطرح
عند جمع او طرح الكميات المناسبة يمكن ان تكون ضباطية النتيجة مساوية فقط لأقل حدود الضباطية في المجموع او الفرق. وفي هذه الحالة تكون كل الارقام وحتى حد الضباطية هذا ارقاما معنوية جميعها.
الأرقام المعنوية في عمليتي الضرب والقسمة
عند ضرب أو طرح الكميات المقاسة يمكن أن يكون عدد الأرقام المعنوية في النتيجة مساوياً فقط لأقل عدد من الأرقام المعنوية في أي عامل في المسألة .
مثال توضيحي:
لنفرض أنك قد أجريت ثلاثة قياسات للطول باستخدام أجهزة ذات ضباطات مختلفة وأنك حصلت على 3.76 cm ، 46.855 ، 0.2 cm . ما مجموع هذا القيم؟
استدلال منطقي :
الحساب :
الآلة الحاسبة تعطي :
ولكن قاعدة الأرقام المعنوية في الجمع والطرح تفيدنا أن النتيجة يجب ان تعطي لأقرب0.1 cm فقط وذلك لأن أقل الكميات ضباطية (0.2) معرفة حتى هذه الضباطية فقط . الإجابة الصحيحة إذن هي50.8 cm.
ولكن نرى ان هذا صحيح بالفعل , لننظر إلى معنى ضباطية كل من الأعداد السابقة. بتطبيق قاعدة ½± سنجد ان القيمة الأولى تقع في المدى من 3.755 إلى 3.765. كذلك فإن القيمة الثانية يمكن ان تكون 46.8555 وهي أكبر قيمة أو 46.8545 وهي أصغر قيمة , أما القيمة الثالثة فتقع في المدى من 0.15 إلى 0.25. ولإيجاد درجة عدم اليقين في المجموع يمكن إيجاد أكبر مجموع باستخدام القيم العليا للأعداد الثلاثة ثم حساب أصغر مجموع باستخدام القيم الصغرى لها :
أكبر مجموع : أصغر مجموع:
ومع ذلك نجد أن مدى اليقين أكبر قليلاً من0.1 cm. هذا المثال التوضيحي يبين أنه حتى الرقم المعنوي الثالث موضع شك ، ومن ثم ليس هناك أي مبرر لادعاء أن الضباطية أعلى من 50.8 cm.
مثال توضيحي:
ما حجم صندوق قيست أطوال أضلاعه فوجد أنها31.3 cm , 28 cm ،51.85 cm ؟
استدلال منطقي :
تذكر أولاً أن حجم الصندوق يمكن إيجاده ضرب طوله في عرضه في ارتفاعه. وباستخدام الآلة الحاسبة نجد أن:
313 cm)(28 cm)(51.85 cm) = 45.441.34 cm3 )-الحجم
ولكن قاعدة الأرقام المعنوية تحتم الاحتفاظ برقمين معنويين فقط ( لأننا محددون برقمين معنويين في القيمة28 cm ) :
45.000 cm3 = 4.5 × 104cm3 -(الحجم)
يبدو أننا قسونا على أنفسنا قسوة شديدة بإهمال جميع الأرقام المعنوية الأخرى. لكن بالنظر إلى معنى الضباطية سنرى أن أكبر قيم للأعداد الثلاثة ، باستعمال معنى الضباطية , هي 31.35 ، 28.5 ، 51.855 . وبذلك سنجد ان القيمة العظمى للحجم هي :
313cm)(28.5 cm)(51.855 cm) = 46.300 cm3) = القيمة العظمى للحجم.
ويمكن إيجاد القيمة الصغرى للحجم باستخدام القيم الصغرى للأعداد المعطاة :
31.25cm)(27.5 cm)(51.845 cm) = 44.600 cm3) = القيمة الصغرى للحجم.
تبين القياسات إذن أن الحجم المحسوب يجب ان يكون في هذا المدى. وهكذا نرى أن الرقم الثاني نفسه غير يقيني ، ومن ثم فإن الحجم يكون 45.000 cm3 تقريباً . وهو يتكون من رقمين معنويين فقط .
تلخيصاً لما سبق من المهم أن نتذكر الآتي :
الحسابات لا يمكنها زيادة ضباطية الكميات المقاسة أو عدد أرقامها المعنوية.
