The properties of oscillators
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
294-297
2025-11-23
35
The properties of oscillators
With the wavefunctions that are available, we can start calculating the properties of a harmonic oscillator. For instance, we can calculate the expectation values of an observable Ω by evaluating integrals of the type
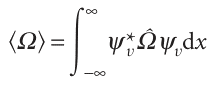
(Here and henceforth, the wavefunctions are all taken to be normalized to 1.) When the explicit wavefunctions are substituted, the integrals look fearsome, but the Hermite polynomials have many simplifying features. For instance, we show in the following example that the mean displacement, x, and the mean square displace ment, x2, of the oscillator when it is in the state with quantum number v are
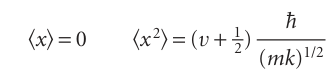
The result for x shows that the oscillator is equally likely to be found on either side of x=0 (like a classical oscillator). The result for x2 shows that the mean square dis placement increases with v. This increase is apparent from the probability densities in Fig. 9.26, and corresponds to the classical amplitude of swing increasing as the oscillator becomes more highly excited.
The mean potential energy of an oscillator, the expectation value of V=1/2kx2, can now be calculated very easily:
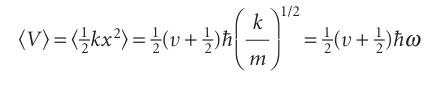
Because the total energy in the state with quantum number v is (v + 1–2)$ω, it follows that
V =1/2Ev
The total energy is the sum of the potential and kinetic energies, so it follows at once that the mean kinetic energy of the oscillator is
EK = 1/2Ev
The result that the mean potential and kinetic energies of a harmonic oscillator are equal (and therefore that both are equal to half the total energy) is a special case of the virial theorem:
If the potential energy of a particle has the form V = axb, then its mean potential and kinetic energies are related by
2(EK) =b(V)
For a harmonic oscillator b = 2, so EK = V, as we have found. The virial theorem is a short cut to the establishment of a number of useful results, and we shall use it again. An oscillator may be found at extensions with V > E that are forbidden by classical physics, for they correspond to negative kinetic energy. For example, it follows from the shape of the wavefunction (see the Justification below) that in its lowest energy state there is about an 8 per cent chance of finding an oscillator stretched beyond its classical limit and an 8 per cent chance of finding it with a classically forbidden com pression. These tunnelling probabilities are independent of the force constant and mass of the oscillator. The probability of being found in classically forbidden regions decreases quickly with increasing v, and vanishes entirely as v approaches infinity, as we would expect from the correspondence principle. Macroscopic oscillators (such as pendulums) are in states with very high quantum numbers, so the probability that they will be found in a classically forbidden region is wholly negligible. Molecules, however, are normally in their vibrational ground states, and for them the probability is very significant.
Justification 9.4 Tunnelling in the quantum mechanical harmonic oscillator According to classical mechanics, the turning point, xtp, of an oscillator occurs when its kinetic energy is zero, which is when its potential energy 1/2kx2 is equal to its total energy E. This equality occurs when
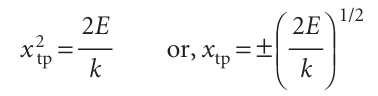
with E given by eqn 9.25. The probability of finding the oscillator stretched beyond a displacement xtp is the sum of the probabilities ψ2dx of finding it in any of the intervals dx lying between xtp and infinity:
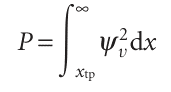
The variable of integration is best expressed in terms of y = x/α with α = (h2/mk)1/2, and then the turning point on the right lies at
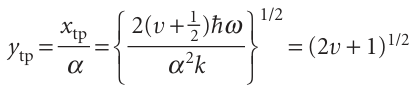
For the state of lowest energy (v = 0), ytp = 1 and the probability is
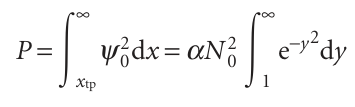
The integral is a special case of the error function, erf z, which is defined as follows:
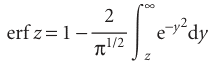
The values of this function are tabulated and available in mathematical software packages, and a small selection of values is given in Table 9.2. In the present case
P= 1/2(1 − erf 1) = 1/2(1 − 0.843) = 0.079
It follows that, in 7.9 per cent of a large number of observations, any oscillator in the state v = 0 will be found stretched to a classically forbidden extent. There is the same probability of finding the oscillator with a classically forbidden compression. The total probability of finding the oscillator tunnelled into a classically forbidden region (stretched or compressed) is about 16 per cent. A similar calculation for the state with v = 6 shows that the probability of finding the oscillator outside the classical turning points has fallen to about 7 per cent.
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
