The qualitative origin of quantized rotation
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
ص297-299
2025-11-23
30
The qualitative origin of quantized rotation
Because Jz =±pr, and, from the de Broglie relation, p = h/λ, the angular momentum about the z-axis is
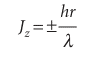
Opposite signs correspond to opposite directions of travel. This equation shows that the shorter the wavelength of the particle on a circular path of given radius, the greater the angular momentum of the particle. It follows that, if we can see why the wavelength is restricted to discrete values, then we shall understand why the angular momentum is quantized. Suppose for the moment that λ can take an arbitrary value. In that case, the wave function depends on the azimuthal angle φ as shown in Fig. 9.28a. When φ increases beyond 2π, the wavefunction continues to change, but for an arbitrary wavelength it gives rise to a different value at each point, which is unacceptable (Section 8.4b). An acceptable solution is obtained only if the wavefunction reproduces itself on successive circuits, as in Fig. 9.28b. Because only some wavefunctions have this property, it follows that only some angular momenta are acceptable, and therefore that only certain rotational energies exist. Hence, the energy of the particle is quantized. Specific ally, the only allowed wavelengths are
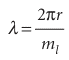
with ml, the conventional notation for this quantum number, taking integral values including 0. The value ml= 0 corresponds to λ =∞; a ‘wave’ of infinite wavelength has a constant height at all values of φ. The angular momentum is therefore limited to the values
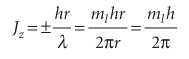
where we have allowed ml to have positive or negative values. That is, Jz = mlh ml = 0, ±1, ±2, ...
Positive values of ml correspond to rotation in a clockwise sense around the z-axis (as viewed in the direction of z, Fig. 9.29) and negative values of ml correspond to counter-clockwise rotation around z. It then follows from eqn 9.36 that the energy is limited to the values
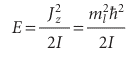
We shall see shortly that the corresponding normalized wavefunctions are
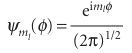
The wavefunction with ml = 0 is ψ0(φ) = 1/(2π)1/2, and has the same value at all points on the circle. We have arrived at a number of conclusions about rotational motion by combining some classical notions with the de Broglie relation. Such a procedure can be very useful for establishing the general form (and, as in this case, the exact energies) for a quantum mechanical system. However, to be sure that the correct solutions have been obtained, and to obtain practice for more complex problems where this less formal approach is inadequate, we need to solve the Schrödinger equation explicitly. The formal solution is described in the Justification that follows.
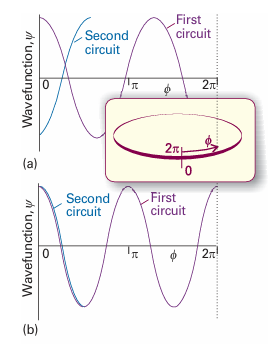
Fig. 9.28 Two solutions of the Schrödinger equation for a particle on a ring. The circumference has been opened out into a straight line; the points at φ = 0 and 2π are identical. The solution in (a) is unacceptable because it is not single valued. Moreover, on successive circuits it interferes destructively with itself, and does not survive. The solution in (b) is acceptable: it is single-valued, and on successive circuits it reproduces itself.
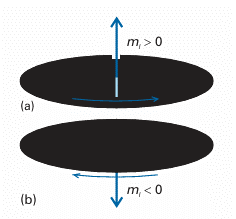
Fig. 9.29 The angular momentum of a particle confined to a plane can be represented by a vector of length |ml | units along the z-axis and with an orientation that indicates the direction of motion of the particle. The direction is given by the right-hand screw rule.
Justification 9.5 The energies and wavefunctions of a particle on a ring The hamiltonian for a particle of mass m in a plane (with V = 0) is the same as that given in eqn 9.10:
and the Schrödinger equation is Hψ = Eψ, with the wavefunction a function of the angle φ. It is always a good idea to use coordinates that reflect the full symmetry of the system, so we introduce the coordinates r and φ (Fig. 9.30), where x = r cos φ and y =rsinφ. By standard manipulations (see Further reading) we can write
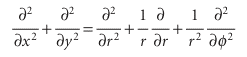
However, because the radius of the path is fixed, the derivatives with respect to r can be discarded. The hamiltonian then becomes
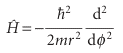
The moment of inertia I = mr2 has appeared automatically, so H may be written
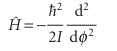
and the Schrödinger equation is
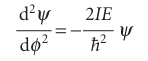
The normalized general solutions of the equation are
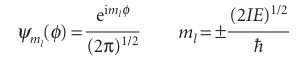
The quantity ml is just a dimensionless number at this stage. We now select the acceptable solutions from among these general solutions by imposing the condition that the wavefunction should be single-valued. That is, the wavefunction ψ must satisfy a cyclic boundary condition, and match at points separated by a complete revolution: ψ (φ + 2π) = ψ(φ). On substituting the general wavefunction into this condition, we find
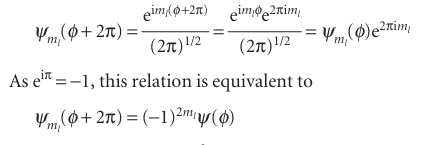
Because we require (−1)2ml = 1, 2ml must be a positive or a negative even integer (including 0), and therefore ml must be an integer: ml = 0, ±1, ±2,....
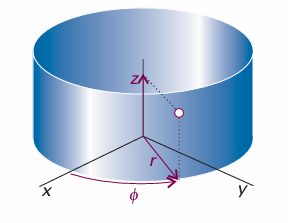
Fig. 9.30 The cylindrical coordinates z, r, and φ for discussing systems with axial (cylindrical) symmetry. For a particle confined to the xy-plane, only r and φ can change.
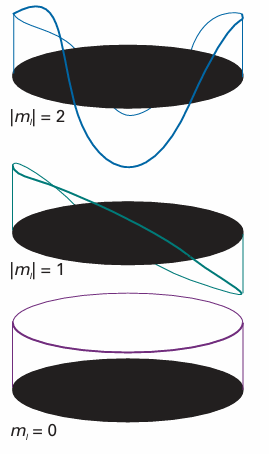
Fig. 9.31 The real parts of the wavefunctions of a particle on a ring. As shorter wavelengths are achieved, the magnitude of the angular momentum around the z-axis grows in steps of $.
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
