In this section we prove an important principle about real numbers that is often used as an axiom in place of Axiom C.

Definitions

A set S of real numbers has the upper bound M if x ≤ M for every number x in S; we also say that the set S is bounded above by M. The set S has the lower bound m if x ≥ m for every number x in S; we also say that S is bounded below by m. A set S is bounded if S has an upper and a lower bound. Suppose that f is a function on R¹ whose domain D contains the set S. We denote by f |S the restriction of to the set S; that is, f |S has domain S and f |S(x) f(x) for all x in S. A function f is bounded above, bounded below, or bounded if the set R consisting of the range of f satisfies the corresponding condition.

 Suppose we define

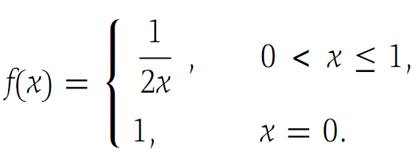
Then f is not bounded on S ={x :0 ≤ x ≤ 1}. See Figure 1.1.

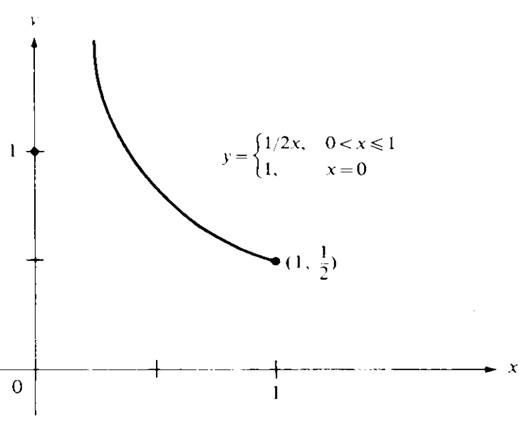
 Figure 1.1

We now prove the fundamental principle on upper and lower bounds (see Figure 1.2).

Figure 1.2 U is the least upper bound for S.

Theorem 1.1

If a nonempty set S ⊂ R¹ has an upper bound M, then it has a least upper bound U; that is, there is a unique number U that is an upper bound for S but is such that no number U^`<U is an upper bound for S. If a nonempty set has a lower bound m, it has a greatest lower bound L.

Proof

The second statement follows by applying the first to the set S^/={x :−x ∈ S}.We prove the first statement using the Nested intervals theorem.

If M ∈ S, then we may take U= M, since in this case every x in S is less than or equal to U, and if U^/<U, then U^/is not an upper bound, since U ∈ S and U>U^/.If M is not in S, let b₁ =M and choose a₁ as any point of S. Now, either (a₁ + b₁)/2 is greater than every x in S, or there is some x in S greater than or equal to (a₁ + b₁)/2. In the first case, if we define a₂ = a₁ and b₂ = (a₁ + b₁)/2, then a₂ ∈ S  and b₂ is greater than every x in S. In the second case, choose for a2 one of the numbers in S that is greater than or equal to (a₁ + b₁)/2 and set b₂ = b₁; then we again have a₂ ∈ S and b₂ greater than every x in S. Continuing in this way, we define an infinite sequence {[a_n,b_n]} of closed intervals such that(1.2)

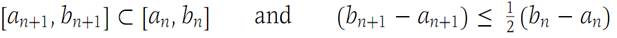
for each n, and so for each n,(1,3)

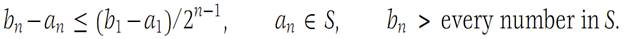
From the Nested intervals theorem, it follows that there is a unique number U in all these intervals and

Let x be any number in S. Then x<b_n for each n, so that x ≤ U by the limit of inequalities. Thus U is an upper bound for S. But now let U^/<U and let ε = U – U^/ . Then, since a_n → U, it follows that there is an N such that U^/=U − ε<a_n ≤ U for all n>N. But since all the an ∈ S, it is clear that U^/ is not an upper bound. Therefore, U is unique.

Definitions

The number U in Theorem 1.1, the least upper bound, is also called the supremum of S and is denoted by

l. u .b. S or sup S.

The number L of Theorem 1.1, the greatest lower bound, is also called the infimum of S and is denoted by

g. l .b. S or in f S.

Corollary

If x₀ is the largest number in S, that is, if x₀ ∈ S and x₀ is larger than every other number in S, then x₀ = sup S. If S is not empty and U= sup S, with U not in S, then there is a sequence {x_n} such that each x_n is in S and x_n → U. Also, if ε> 0 is given, there is a_n x in S such that  x>U − ε. Corresponding results hold for in f S.

These results follow from the definitions and from the proof of Theorem 1.1 With the help of this corollary it is possible to show that the Axiom of Continuity is a consequence of Theorem 1.1.

Definitions

Let f have an interval I of R¹ as its domain and a set in R¹ as its range.

We say that f is increasing on I if f(x₂)>f(x₁) whenever x₂ >x₁. The

function f is non decreasing on I if f(x₂) ≥ f(x₁) whenever x₂ >x₁. The

function f is decreasing on I if f(x₂)<f(x₁) whenever x₂ >x₁. The

function f is non increasing on I if f(x₂) ≤ f(x₁) whenever x₂ >x₁.A

function that has any one of these four properties is called monotone

on I.

Monotone functions are not necessarily continuous, as the following step function exhibits:

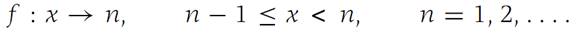
See Figure 1.3. Also, monotone functions may not be bounded. The function f : x → 1/(1 − x) is monotone on the interval I ={x :0 ≤ x< 1} but is not bounded there.

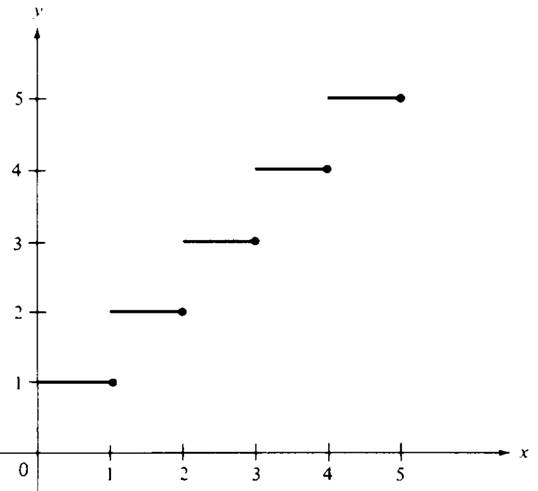
Figure 1.3 A step function.

If a function f defined on an interval I is continuous on I, then an extension of the Intermediate-value theorem shows that the range of f is an interval. In order to establish this result, we use the following characterization of an interval on R¹.

Theorem 1.2

A set S in R¹is an interval ⇔ (i) S contains more than one point and (ii) for every x₁,x₂ ∈ S the number x is in S whenever x ∈ (x₁,x₂).

Proof

If S is an interval, then clearly the two properties hold. Therefore, we suppose that (i) and (ii) hold and show that S is an interval. We consider two cases.

Case 1: S is bounded. Define a = inf S and b =sup S. Let x be an element of the open interval (a, b). We shall show that x ∈ S.

Since a = inf S, we use the corollary to Theorem 1.1 to assert that there is an x₁ ∈ S with x₁ <x. Also, since b = sup S, there is an x₂ in S with x₂ >x. Hence x ∈ (x₁,x₂), which by (ii) of the hypothesis shows that x ∈ S. We conclude that every element of (a, b) is in S. Thus S is either a closed interval, an open interval, or a half-open interval; its endpoints are a, b.

Case 2: S is unbounded in one direction. Assume that S is unbounded above and bounded below, the case of S bounded above and unbounded below being similar. Let a= inf S. Then S ⊂ [a,∞). Let x be any number such that x>a. We shall show that x ∈ S. As in Case 1, there is a number x₁ ∈ S such that x₁ <x. Since S has no upper bound there is an x₂ ∈ S such that x₂ >x. Using (ii) of the hypothesis, we conclude that x ∈ S. Therefore, S = [a,∞) or S= (a,∞).

We now establish a stronger form of the Intermediate-value theorem.

Theorem 1.3

Suppose that the domain of f is an interval I and f is continuous on I. Assume that f is not constant on I. Then the range of f , denoted by J , is an interval.

Proof

We shall show that J has properties(i) and (ii) of Theorem 1.2 and therefore is an interval. Since f is not constant, its range must have more than one point, and property (i) is established. Now let y₁,y₂ ∈ J . Then there are numbers x₁,x₂ ∈ I such that f(x₁) = y₁ and f(x₂) = y₂. We may assume that x₁ <x₂. The function f is continuous on [x₁,x₂], and so we may apply the Intermediate-value theorem. If c is any number between y₁ and y₂, there is an x₀ ∈ [x₁,x₂] such that f(x₀) = c. Thus c ∈ J , and we have established property (ii). The set J is an interval.

If f is continuous on I ={x : a ≤ x ≤ b}, it is not necessarily the case that J is determined by f(a) and f(b). Figure 1.4 shows that J may exceed the interval [f(a), f(b)]. In fact, I may be bounded and J unbounded, as is illustrated by the function f : x → 1/x with I ={x :0 <x< 1}.The range is J ={y :1 <y< ∞}. The function f : x → 1/(1 + x2) with I ={x :0 <x< ∞} and J ={y :0 <y< 1} is an example of a continuous function with an unbounded domain and a bounded range.

Consider the restriction to [0,∞) of the function f : x → x_n where n is a positive integer. By Theorem1.3, the range of f is an interval, which must be [0,∞), since f(0) = 0, f is increasing, and f(x) →+∞ as x →+∞.

Hence, for each x ≥ 0, there isat least one number y ≥ 0 such that y_n = x. If y^/>y, then (y^/)n >y_n = x. Also, if 0 ≤ y^/<y, then (y^/)n <x.

Thus the solution y is unique. We denote it by x₁/n. Every positive number has an nth root for every positive integer n. The function x → x₁/n, x ≥ 0, can be shown to be continuous on [0,∞).

Figure 1.4

Problems

In Problems1 through 8 find l.u.b. S and g.l.b. S. State whether or not these numbers are in S.

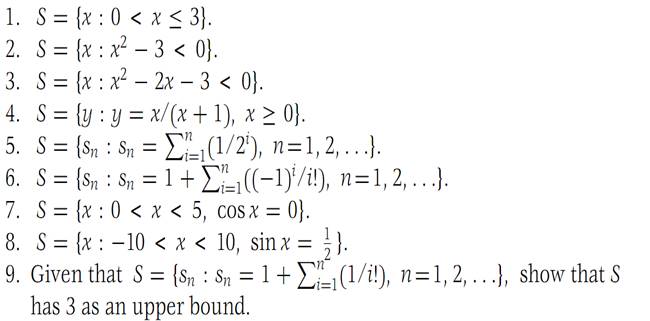
Basic Elements of Real Analysis, Murray H. Protter, Springer, 1998 .Page(44-53)

اخر الاخبار

اخبار العتبة العباسية المقدسة

معهد القرآن الكريم النسوي ينظّم سفرة دينية إلى كربلاء المقدسة لطالبات الدورات القرآنية الصيفية

العتبة العباسية المقدسة تناقش مع هيأة الإعلام والاتصالات تسهيل عمل المؤسّسات الصحفية لتغطية زيارة عاشوراء

لليوم الخامس.. العتبة العباسية المقدسة تواصل إقامة مجلس عزائها المركزي في الصحن الشريف

قسم الشؤون الدينية يفتتح موكبًا لخدمة زائري مدينة كربلاء في شهر المحرم

المزيد

الآخبار الصحية

لمن تجاوز الستين.. عليك بشرب 4 أكواب من القهوة يوميا ؟

الحليب مع العسل.. مزيج يمنحك 7 فوائد صحية

لا تبالغ في التنظيف.. قليل من "الاتساخ" قد يحمي عائلتك

دراسة تكشف علاقة خطيرة بين عمر الأم وصحة مولودها

المزيد

الآخبار التكنلوجية

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

كيف تساعد الصيانة الوقائية في الحفاظ على كفاءة التكييف في سيارتك ؟

في ظاهرة غريبة حيرت العلماء.. كوكبنا قد يسجل أقصر يوم في التاريخ هذا الصيف!

المزيد

مواضيع ذات صلة

Elementary Theory of Metric Spaces-The Schwarz and Triangle Inequalities; Metric Spaces

Elementary Theory of Metric Spaces-Functions on Compact Sets

Elementary Theory of integration -The Darboux Integral for Functions on RN

Elementary Theory of integration -The Logarithm and Exponential Functions

Elementary Theory of integration -The Riemann Integral

Differentiation and Integration in RN-The Riemann Integral in RN

Differentiation and Integration in RN-The Darboux Integral in RN

Differentiation and Integration in RN-The Derivative in RN

Differentiation and Integration in RN-Taylor,s Theorem; Maxima and Minima

Differentiation and Integration in RN-Partial Derivatives and the Chain Rule

Continuity

Basic Properties of Functions on R1 -The Heine–Borel Theorem