We recall the definition of a convergent sequence x₁,x₂,...,x_n,....A sequence converges to a limit L if for every ε> 0 there is a positive integer N such that

(1.8)                      |x_n − L| <ε       whenever      n>N.

| − |

Suppose we are given a sequence and wish to examine the possibility of convergence. Usually the number L is not given, so that condition (1.8) above cannot be verified directly. For this reason it is important to have a technique for deciding convergence that doesn’t employ the limit L of the sequence. Such a criterion, presented below, was given first by Cauchy.

Definition

An infinite sequence {x_n} is called a Cauchy sequence if and only if for each ε> 0, there is a positive integer N such that |x_n − x_m| <ε for all m>N and all n>N.

Theorem 1.1 (Cauchy criterion for convergence)

A necessary and sufficient condition for convergence of a sequence {x_n} is that it be a Cauchy sequence.

Proof

We first show that if {x_n} is convergent, then it is a Cauchy sequence. Suppose L is the limit of {x_n}, and let ε> 0 be given. Then from the definition of convergence there is an N such that

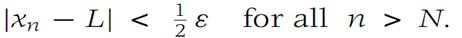
Let x_m be any element of {x_n} with m>N. We have

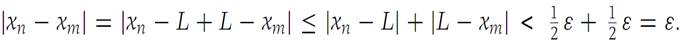
Thus {x_n} isa Cauchy sequence.

Now assume that {x_n} is a Cauchy sequence; we wish to show that it Is convergent. We first prove that {x_n} is a bounded sequence. From the definition of Cauchy sequence with ε = 1, there is an integer N0 such that

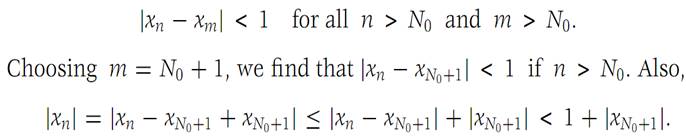
Keep N₀ fixed and observe that all |x_n| beyond x_N0 are bounded by 1 + |x_N0+1|, a fixed number. Now examine the finite sequence of numbers |x₁|, |x₂|,..., |x_N0 |, |x_N0+1|+ 1

and denote by M the largest of these. Therefore, |x_n|≤ M for all positive integers n, and so {x_n} is a bounded sequence. We now apply the Bolzano–Weierstrass theorem  and conclude that there is a subsequence {x_kn } of {x_n} that converges to some limit L. We shall show that the sequence {x_n} itself converges to L. Let ε> 0 be given. Since {x_n} is a Cauchy sequence, there is an N₁ such that

Also, since {x_kn } converges to L, there is an N₂ such that

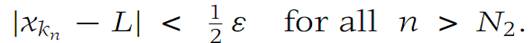
Let N be the larger of N1 and N2, and consider any integer n larger than N.We recall from the definition of subsequence of a sequence that k_n ≥ n for every n. Therefore,

Since this inequality holds for all n>N, the sequence {x_n} converges to L.

As an example, we show that the sequence x_n = (cos nπ)/n,   n= 1, 2,..., is a Cauchy sequence. Let ε> 0 be given. Choose N to be any integer larger than 2/ε. Then we have

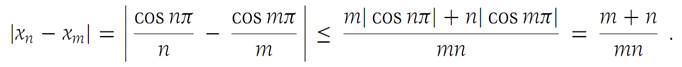
If m>n, we may write

However, because n>N, we have n> 2/ε, and so |x_n − x_m| <ε, and the sequence is a Cauchy sequence.

Basic Elements of Real Analysis, Murray H. Protter, Springer, 1998 .Page(61-63)

اخر الاخبار

اخبار العتبة العباسية المقدسة

خمسون عامًا من العطاء.. نجم الأعرجي خادم الزائرين بلا انقطاع

العتبة العباسية المقدسة تواصل إقامة مجالسها العزائية لإحياء شهر المحرم

العتبة العباسية المقدسة تطلق سلسلة محاضرات قرآنية عاشورائية في بابل

في مساء اليوم الخامس من المحرّم.. المواكب الكربلائيّة تواصل فعالياتها العزائية

المزيد

الآخبار الصحية

لهذا السبب.. إغلاق 25 مركزًا لعلاج الإدمان في مصر ؟

خلافا للاعتقاد الشائع.. علماء يكشفون أسرار بذور البطيخ ؟!

هذا ما يحدث لجسمك عند تناولك الطماطم بانتظام !

تعرف على أطعمة تسرّع "تعافي الجسم" من حروق الشمس

المزيد

الآخبار التكنلوجية

الثلوج تغطي الصحراء الأكثر جفافا في العالم!

بتلسكوب "ألما".. التقاط صورا غير مسبوقة لبدايات الكون !

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

المزيد

مواضيع ذات صلة

Elementary Theory of Metric Spaces-The Schwarz and Triangle Inequalities; Metric Spaces

Elementary Theory of Metric Spaces-Functions on Compact Sets

Elementary Theory of integration -The Darboux Integral for Functions on RN

Elementary Theory of integration -The Logarithm and Exponential Functions

Elementary Theory of integration -The Riemann Integral

Differentiation and Integration in RN-The Riemann Integral in RN

Differentiation and Integration in RN-The Darboux Integral in RN

Differentiation and Integration in RN-The Derivative in RN

Differentiation and Integration in RN-Taylor,s Theorem; Maxima and Minima

Differentiation and Integration in RN-Partial Derivatives and the Chain Rule

Continuity

Basic Properties of Functions on R1 -The Heine–Borel Theorem