In the definition of continuity of a function f at a point x₀, it is necessary to obtain a number δ for each positive number ε prescribed in advance  The number δ, which naturally depends on ε, also depends on the particular value x₀. Under certain circumstances it may happen that the same value δ may be chosen for all points x in the domain. Then we say that f is uniformly continuous.

Definition

A function f with domain S is said to be uniformly continuous on S if for every ε> 0 there is a δ> 0 such that

                        |f(x₁) − f(x₂)| <ε    whenever  |x₁ − x₂| <δ

and   x₁,x₂  are in S. The important condition of uniform continuity states that the same value of δ holds for all x₁,x₂ in S.

Among the properties of continuous functions used in proving the basic theorems of integral calculus, that of uniform continuity plays a central role. The principal result of this section (Theorem 1.1 below) shows that under rather simple hypotheses continuous functions are uniformly continuous.

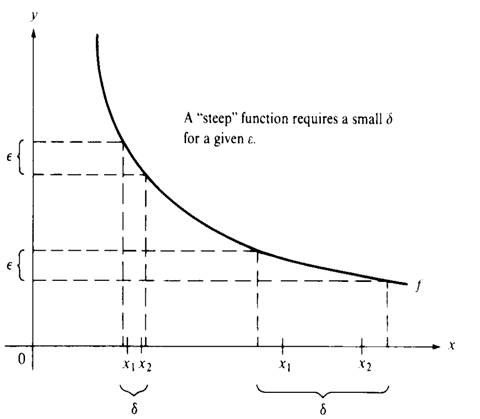
                                                   Figure 1.1

A function may be continuous on a set S without being uniformly continuous. As Figure 1.1 shows, once an ε is given, the value of δ required n the definition of ordinary continuity varies according to the location of x₁ and x₂; the “steeper” the function, the smaller the value of δ required. As an example of a continuous function that is not uniformly continuous, consider

defined on the set S ={x :0 <x ≤ 1}. It is clear that f is continuous for each x in S. However, with ε any positive number, say 1, we shall show

there is no number δ such that

                             |f(x₁) − f(x₂)| < 1 whenever |x₁ − x₂| <δ

for all x₁,x₂ in S. To see this we choose x₁ = 1/n and x₂ = 1/(n + 1) for a positive integer n. Then |f(x₁) − f(x₂)|=|n − (n + 1)|= 1; also, we have |x₁ − x₂|= 1/(n(n + 1)).If n is very large, then x₁ and x₂ are close together. Therefore, if a δ is given, simply choose n so large that x₁ and x₂ are closer together than δ. The condition of uniform continuity is violated, since f(x₁) and f(x₂) may not be “close.”

An example of a uniformly continuous function on a set S is given by(1.6)

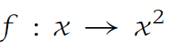
on the domain S ={x :0 ≤ x ≤ 1}. To see this, suppose ε> 0 is given.

We must find a δ> 0 such that

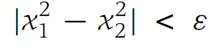
whenever |x₁ − x₂| <δ

for all x₁,x₂ in S. To accomplish this, choose δ = ε/2. Then, because 0 ≤ x1 ≤ 1 and 0 ≤ x2 ≤ 1, we have

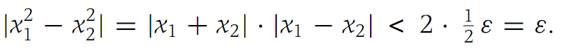
This inequality holds for all x₁,x₂ on [0, 1] such that |x₁ − x₂| <δ.

The same function (1.6) above defined on the domain S₁ ={x :0 ≤ x< ∞} is not uniformly continuous there. To see this, suppose ε> 0 Is given. Then for any δ> 0, choose x₁,x₂ such that x₁ − x₂ = δ/2 and x₁ + x₂ = 4ε/δ. Then we have

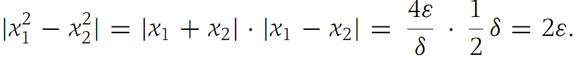
The condition of uniform continuity is violated for this x₁,x₂. An important criterion for determining when a function is uniformly continuous is established in the next result.

Theorem 1.1 (Uniform continuity Theorem)

If f is continuous on the closed interval I ={x:a ≤ x ≤ b}, then f is uniformly continuous on I.

Proof

We shall suppose that f is not uniformly continuous on I and reach a contradiction. If f is not uniformly continuous, there is an ε0 > 0for which there is no δ> 0 with the property that |f(x₁) − f(x₂)| <ε0 for all pairs x₁,x₂ ∈ I and such that |x₁ − x₂| <δ. Then for each positive integer n, there is a pair x^/_n,x^//_n on I such that(1.7)

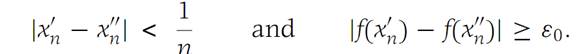
From the Bolzano–Weierstrass theorem, it follows that there is a subse-quence of {x^/_n}, which we denote {x^/_kn}, convergent to some number x₀ in I. Then, since |x^/_kn− x^//_kn| < 1/n, we see that x^//_kn→ x₀ as n →∞. Using the fact that f is continuous on I, we havef(x^/_kn) → f(x₀), f(x^//_kn) → f(x₀).

That is, there are positive integers N1 and N2 such that

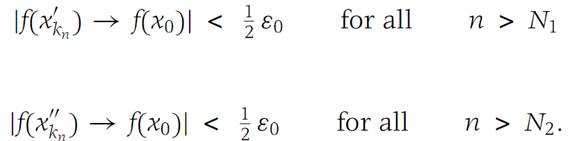
Hence for all n larger than both N₁ and N₂ we find

This last inequality contradicts (1.7), and the result is established. As the example of the function f : x → 1/x shows, the requirement that I be a closed interval is essential. Also, the illustration of the function f : x → x₂ on the set S₁ ={x :0 ≤ x< ∞} shows that Theorem1.11 does not apply if the interval is unbounded. It may happen that continuous functions are uniformly continuous on unbounded sets. But these must be decided on a case-by-case basis. See Problems 3 and 4 at the end of the section.

Problems

1. Suppose that f is a continuous, increasing function on a closed interval    I ={x : a ≤ x ≤ b}. Show that the range of f is the interval [f(a), f(b)].

2. Suppose that f is uniformly continuous on the closed intervals I₁

and I₂. Show that f is uniformly continuous on S = I₁ ∪ I₂.

3. Show that the function f : x → 1/x is uniformly continuous on S ={x :1 ≤ x< ∞}.

Basic Elements of Real Analysis, Murray H. Protter, Springer, 1998 .Page(57-60)

اخر الاخبار

اخبار العتبة العباسية المقدسة

خمسون عامًا من العطاء.. نجم الأعرجي خادم الزائرين بلا انقطاع

العتبة العباسية المقدسة تواصل إقامة مجالسها العزائية لإحياء شهر المحرم

العتبة العباسية المقدسة تطلق سلسلة محاضرات قرآنية عاشورائية في بابل

في مساء اليوم الخامس من المحرّم.. المواكب الكربلائيّة تواصل فعالياتها العزائية

المزيد

الآخبار الصحية

لهذا السبب.. إغلاق 25 مركزًا لعلاج الإدمان في مصر ؟

خلافا للاعتقاد الشائع.. علماء يكشفون أسرار بذور البطيخ ؟!

هذا ما يحدث لجسمك عند تناولك الطماطم بانتظام !

تعرف على أطعمة تسرّع "تعافي الجسم" من حروق الشمس

المزيد

الآخبار التكنلوجية

الثلوج تغطي الصحراء الأكثر جفافا في العالم!

بتلسكوب "ألما".. التقاط صورا غير مسبوقة لبدايات الكون !

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

المزيد

مواضيع ذات صلة

Elementary Theory of Metric Spaces-The Schwarz and Triangle Inequalities; Metric Spaces

Elementary Theory of Metric Spaces-Functions on Compact Sets

Elementary Theory of integration -The Darboux Integral for Functions on RN

Elementary Theory of integration -The Logarithm and Exponential Functions

Elementary Theory of integration -The Riemann Integral

Differentiation and Integration in RN-The Riemann Integral in RN

Differentiation and Integration in RN-The Darboux Integral in RN

Differentiation and Integration in RN-The Derivative in RN

Differentiation and Integration in RN-Taylor,s Theorem; Maxima and Minima

Differentiation and Integration in RN-Partial Derivatives and the Chain Rule

Continuity

Basic Properties of Functions on R1 -The Heine–Borel Theorem