Kelvin Functions

Kelvin defined the Kelvin functions bei and ber according to

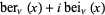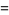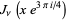			(1)
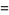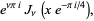			(2)
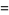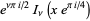			(3)
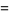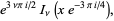			(4)

where 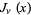 is a Bessel function of the first kind and  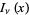is a modified Bessel function of the first kind. These functions satisfy the Kelvin differential equation.

Similarly, the functions kei and ker by

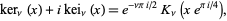(5)

where 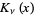 is a modified Bessel function of the second kind. For the special case ,

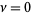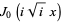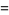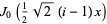			(6)
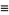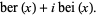			(7)

REFERENCES:

Abramowitz, M. and Stegun, I. A. (Eds.). "Kelvin Functions." §9.9 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 379-381, 1972.

Prudnikov, A. P.; Marichev, O. I.; and Brychkov, Yu. A. "The Kelvin Functions 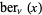, , 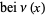 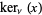and 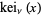." §1.7 in Integrals and Series, Vol. 3: More Special Functions. Newark, NJ: Gordon and Breach, pp. 29-30, 1990.

Spanier, J. and Oldham, K. B. "The Kelvin Functions." Ch. 55 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 543-554, 1987.