المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Slater,s Formula |
 1778
 06:28 مساءً
date: 18-6-2019 |
Author : Slater, L. J. 
Book or Source : "An Elementary Proof of the _4F_3[1] Summation Theorem." §2.7.1 in Confluent Hypergeometric Functions. Cambridge, England: Cambridge University Press 
Page and Part : p. 31|
Read More
Date: 28-8-2019
1792
Date: 16-4-2019
2427
Date: 5-9-2019
1391
|
![_4F_3[a,1+1/2a,b,-n; 1/2a,1+a-b;1+a+n]=((1+a)_n(1/2+1/2a-b)_n)/((1/2+1/2a)_n(1+a-b)_n)](http://mathworld.wolfram.com/images/equations/SlatersFormula/NumberedEquation1.gif) |
for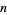 
a nonnegative integer the "![_4F_3[1]](http://mathworld.wolfram.com/images/equations/SlatersFormula/Inline2.gif)
summation theorem." Here,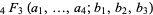 
is a generalized hypergeometric function with argument 
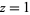and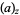 
is a Pochhammer symbol.
This is a special case of the more general identity
 |
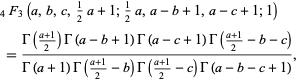which holds for ![R[a-2b-2b]>-1](http://mathworld.wolfram.com/images/equations/SlatersFormula/Inline6.gif)
(O. Marichev, pers. comm., May 16, 2008).
REFERENCES:
Slater, L. J. "An Elementary Proof of the ![_4F_3[1]](http://mathworld.wolfram.com/images/equations/SlatersFormula/Inline7.gif)
Summation Theorem." §2.7.1 in Confluent Hypergeometric Functions. Cambridge, England: Cambridge University Press, p. 31, 1960.
|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|
