Rational Amicable Pair

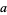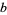A rational amicable pair consists of two integers  and  for which the divisor functions are equal and are of the form

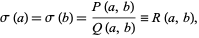(1)

where 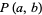 and 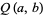 are bivariate polynomials, and for which the following properties hold (Y. Kohmoto):

1. All the degrees of terms of the numerator of the right fraction are the same.

2. All the degrees of terms of the denominator of the right fraction are the same.

3. The degree of  is one greater than the degree of .

If 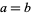 and 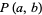 is of the form 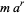, then (◇) reduces to the special case

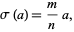(2)

so if 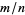 is an integer, then  is a multiperfect number.

Consider polynomials of the form

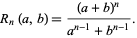(3)

For , (◇) reduces to

(4)

of which no examples are known. For 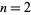, (◇) reduces to

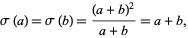(5)

so 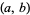 form an amicable pair. For 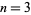, (◇) becomes

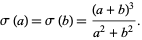(6)

Kohmoto has found three classes of solutions of this type. The first is

(7)

where 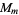 is a Mersenne prime with 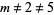, giving (26403469440047700, 30193441130006700), (7664549986025275200, 8764724625167659200), ... (OEIS A038362 and A038363). The second set of solutions is

(8)

where 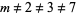, giving the solution

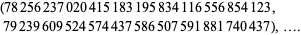(9)

The third type is the unique solution

(10)

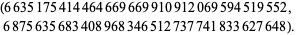(11)

Considering polynomials of the more general form

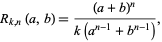(12)

Kohmoto has found the 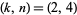 solution

(13)

for 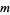 the index of a Mersenne prime with the exceptions of  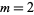and 3.

Kohmoto (pers. comm., Feb. 2004) also found the 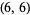 solution

(14)

for 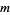 the index of a Mersenne prime with the exceptions of .

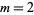Considering polynomials of the form

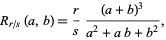(15)

for 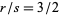, Kohmoto has found the solution

(16)

Considering polynomials of the form

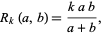(17)

or equivalently,

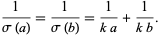(18)

Kohmoto has found the solutions listed in the following table.

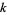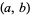6	(1537536, 2269696)
8	(22405565952, 21500290560)
9	(8509664043532288000, 5783455883132928000)

REFERENCES:

Sloane, N. J. A. Sequences A038362 and A038363 in "The On-Line Encyclopedia of Integer Sequences."