


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 19-9-2020
Date: 24-12-2019
Date: 23-2-2020
|

A figurate number, also (but mostly in texts from the 1500 and 1600s) known as a figural number (Simpson and Weiner 1992, p. 587), is a number that can be represented by a regular geometrical arrangement of equally spaced points. If the arrangement forms a regular polygon, the number is called a polygonal number. The polygonal numbers illustrated above are called triangular, square, pentagonal, and hexagonal numbers, respectively. Figurate numbers can also form other shapes such as centered polygons, L-shapes, three-dimensional solids, etc.
The 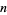 th regular
th regular 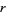 -polytopic number is given by
-polytopic number is given by
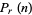 |
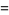 |
 |
(1) |
 |
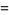 |
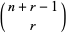 |
(2) |
 |
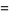 |
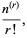 |
(3) |
where  is the multichoose function,
is the multichoose function, 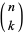 is a binomial coefficient, and
is a binomial coefficient, and 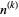 is a rising factorial. Special cases therefore include the triangular numbers
is a rising factorial. Special cases therefore include the triangular numbers
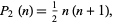 |
(4) |
tetrahedral numbers
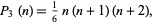 |
(5) |
pentatope numbers
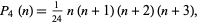 |
(6) |
and so on (Dickson 2005, p. 7).
The following table lists the most common types of figurate numbers.
| figurate number | formula |
| biquadratic number | 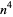 |
| centered cube number | 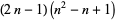 |
| centered pentagonal number | 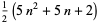 |
| centered square number | 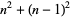 |
| centered triangular number | 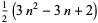 |
| cubic number | 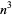 |
| decagonal number | 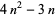 |
| gnomonic number | 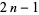 |
| Haűy octahedral number | 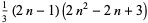 |
| Haűy rhombic dodecahedral number | 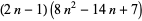 |
| heptagonal number | 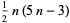 |
| hex number | 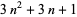 |
| heptagonal pyramidal number | 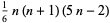 |
| hexagonal number | 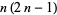 |
| hexagonal pyramidal number | 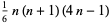 |
| octagonal number | 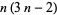 |
| octahedral number | 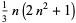 |
| pentagonal number | 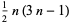 |
| pentagonal pyramidal number | 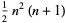 |
| pentatope number | 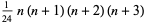 |
| pronic number | 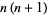 |
| rhombic dodecahedral number | 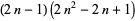 |
| square number | 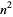 |
| square pyramidal number | 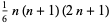 |
| stella octangula number | 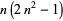 |
| tetrahedral number | 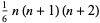 |
| triangular number | 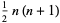 |
| truncated octahedral number | 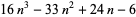 |
| truncated tetrahedral number | 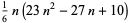 |
REFERENCES:
Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 30-62, 1996.
Dickson, L. E. "Polygonal, Pyramidal, and Figurate Numbers." Ch. 1 in History of the Theory of Numbers, Vol. 2: Diophantine Analysis. New York: Chelsea, pp. 1-39, 2005.
Goodwin, P. "A Polyhedral Sequence of Two." Math. Gaz. 69, 191-197, 1985.
Guy, R. K. "Figurate Numbers." §D3 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 147-150, 1994.
Kraitchik, M. "Figurate Numbers." §3.4 in Mathematical Recreations. New York: W. W. Norton, pp. 66-69, 1942.
Savin, A. "Shape Numbers." Quantum 11, 14-18, 2000.
Simpson, J. A. and Weiner, E. S. C. (Preparers). The Compact Oxford English Dictionary, 2nd ed. Oxford, England: Clarendon Press, 1992.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|