
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 30-6-2020
Date: 13-9-2020
Date: 25-3-2020
|
A number which is simultaneously a nonagonal number 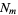 and hexagonal number
and hexagonal number 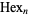 and therefore satisfies the Diophantine equation
and therefore satisfies the Diophantine equation
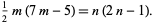 |
(1) |
Completing the square and rearranging gives
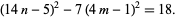 |
(2) |
Defining 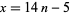 and
and 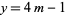 gives the Pell-like equation
gives the Pell-like equation
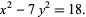 |
(3) |
This has fundamental solutions 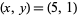 , (9, 3), and (19, 17), giving the family of solutions (5, 1), (9, 3), (19, 17), (61, 23), (135, 51), (509, 193), .... These give solutions which are integers in
, (9, 3), and (19, 17), giving the family of solutions (5, 1), (9, 3), (19, 17), (61, 23), (135, 51), (509, 193), .... These give solutions which are integers in 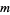 and
and 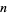 of
of 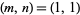 , (10, 13), (39025, 51625), ... (OEIS A048916 and A048917), giving the nonagonal hexagonal numbers 1, 325, 5330229625, 1353857339341, 22184715227362706161, ... (OEIS A048918).
, (10, 13), (39025, 51625), ... (OEIS A048916 and A048917), giving the nonagonal hexagonal numbers 1, 325, 5330229625, 1353857339341, 22184715227362706161, ... (OEIS A048918).
REFERENCES:
Sloane, N. J. A. Sequences A048916, A048917, and A048918 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
هل تعرف كيف يؤثر الطقس على ضغط إطارات سيارتك؟ إليك الإجابة
|
|
|
|
|
|
|
معهد القرآن الكريم النسوي يقدم خدماته لزائري الإمام الكاظم (عليه السلام)
|
|
|