


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 15-1-2020
Date: 22-5-2020
Date: 28-12-2020
|

Clark's triangle is a number triangle created by setting the vertex equal to 0, filling one diagonal with 1s, the other diagonal with multiples of an integer  , and filling in the remaining entries by summing the elements on either side from one row above. The illustration above shows Clark's triangle for
, and filling in the remaining entries by summing the elements on either side from one row above. The illustration above shows Clark's triangle for 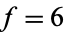 (OEIS A090850).
(OEIS A090850).
Call the first column 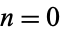 and the last column
and the last column 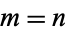 so that
so that
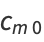 |
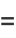 |
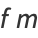 |
(1) |
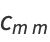 |
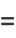 |
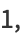 |
(2) |
then use the recurrence relation
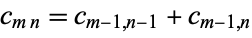 |
(3) |
to compute the rest of the entries. The result is given analytically by
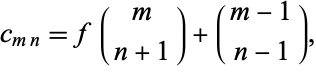 |
(4) |
where 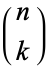 is a binomial coefficient (M. Alekseyev, pers. comm., Aug. 10, 2005).
is a binomial coefficient (M. Alekseyev, pers. comm., Aug. 10, 2005).
The interesting part is that if 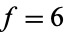 is chosen as the integer, then
is chosen as the integer, then 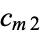 and
and 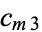 simplify to
simplify to
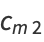 |
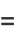 |
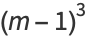 |
(5) |
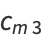 |
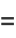 |
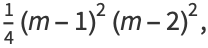 |
(6) |
which are consecutive cubes 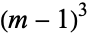 and nonconsecutive squares
and nonconsecutive squares ![n^2=[(m-1)(m-2)/2]^2](https://mathworld.wolfram.com/images/equations/ClarksTriangle/Inline22.gif) .
.
The sum of the 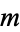 th row for
th row for 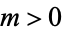 is given by
is given by
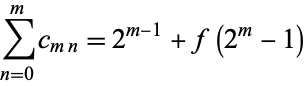 |
(7) |
(M. Alekseyev, pers. comm., Aug. 10, 2005).
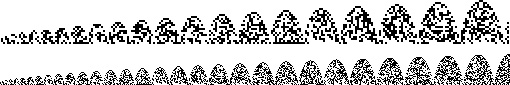
The plot above shows the binary representations for the first 255 (top figure) and 511 (bottom figure) terms of a flattened Clark's triangle with 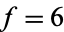 .
.
REFERENCES:
Clark, J. E. "Clark's Triangle." Math. Student 26, No. 2, p. 4, Nov. 1978.
Sloane, N. J. A. Sequence A090850 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
دراسة تكشف "مفاجأة" غير سارة تتعلق ببدائل السكر
|
|
|
|
|
|
|
أدوات لا تتركها أبدًا في سيارتك خلال الصيف!
|
|
|
|
|
|
|
العتبة العباسية المقدسة تؤكد الحاجة لفنّ الخطابة في مواجهة تأثيرات الخطابات الإعلامية المعاصرة
|
|
|