


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 26-1-2017
Date: 20-12-2015
Date: 21-12-2015
|
Counting Degrees of Freedom
Let us now turn to the problem of counting the number of degrees of freedom needed to describe the region y > δ [9].The UV/IR connection implies that this region can be described in terms of an ultraviolet regulated theory with a cutoff length δ. Consider a patch of the boundary with unit coordinate area. Within that patch there are 1/δ3 cutoff cells of size δ. Within each such cell the fields are constant in a cutoff theory. Thus each cell has of order N2 degrees of freedom corresponding to the N ⊗ N components of the adjoint representation of U(N).Th us the number of degrees of freedom on the unit area is
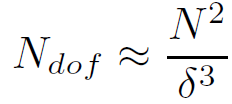 (1.1)
(1.1)
On the other hand the 8-dimensional area of the regulated patch is
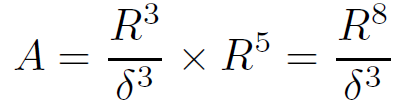 (1.2)
(1.2)
and the number of degrees of freedom per unit area is
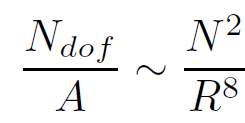 (1.3)
(1.3)
Finally we may
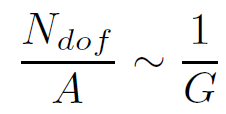 (1.4)
(1.4)
This is very gratifying because it is exactly what is required by the Holographic Principle.



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
في مدينة الهرمل اللبنانية.. وفد العتبة الحسينية المقدسة يستمر بإغاثة العوائل السورية المنكوبة
|
|
|