We recall the definition of a convergent sequence x₁,x₂,...,x_n,....A sequence converges to a limit L if for every ε> 0 there is a positive integer N such that

(1.8)                      |x_n − L| <ε       whenever      n>N.

| − |

Suppose we are given a sequence and wish to examine the possibility of convergence. Usually the number L is not given, so that condition (1.8) above cannot be verified directly. For this reason it is important to have a technique for deciding convergence that doesn’t employ the limit L of the sequence. Such a criterion, presented below, was given first by Cauchy.

Definition

An infinite sequence {x_n} is called a Cauchy sequence if and only if for each ε> 0, there is a positive integer N such that |x_n − x_m| <ε for all m>N and all n>N.

Theorem 1.1 (Cauchy criterion for convergence)

A necessary and sufficient condition for convergence of a sequence {x_n} is that it be a Cauchy sequence.

Proof

We first show that if {x_n} is convergent, then it is a Cauchy sequence. Suppose L is the limit of {x_n}, and let ε> 0 be given. Then from the definition of convergence there is an N such that

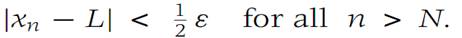
Let x_m be any element of {x_n} with m>N. We have

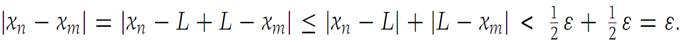
Thus {x_n} isa Cauchy sequence.

Now assume that {x_n} is a Cauchy sequence; we wish to show that it Is convergent. We first prove that {x_n} is a bounded sequence. From the definition of Cauchy sequence with ε = 1, there is an integer N0 such that

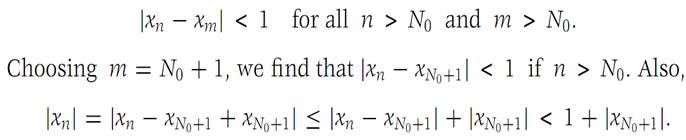
Keep N₀ fixed and observe that all |x_n| beyond x_N0 are bounded by 1 + |x_N0+1|, a fixed number. Now examine the finite sequence of numbers |x₁|, |x₂|,..., |x_N0 |, |x_N0+1|+ 1

and denote by M the largest of these. Therefore, |x_n|≤ M for all positive integers n, and so {x_n} is a bounded sequence. We now apply the Bolzano–Weierstrass theorem  and conclude that there is a subsequence {x_kn } of {x_n} that converges to some limit L. We shall show that the sequence {x_n} itself converges to L. Let ε> 0 be given. Since {x_n} is a Cauchy sequence, there is an N₁ such that

Also, since {x_kn } converges to L, there is an N₂ such that

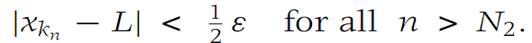
Let N be the larger of N1 and N2, and consider any integer n larger than N.We recall from the definition of subsequence of a sequence that k_n ≥ n for every n. Therefore,

Since this inequality holds for all n>N, the sequence {x_n} converges to L.

As an example, we show that the sequence x_n = (cos nπ)/n,   n= 1, 2,..., is a Cauchy sequence. Let ε> 0 be given. Choose N to be any integer larger than 2/ε. Then we have

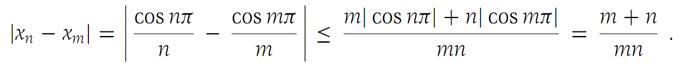
If m>n, we may write

However, because n>N, we have n> 2/ε, and so |x_n − x_m| <ε, and the sequence is a Cauchy sequence.

Basic Elements of Real Analysis, Murray H. Protter, Springer, 1998 .Page(61-63)