


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 5-11-2020
Date: 22-5-2016
Date: 29-10-2020
|
Electrostatics and magnetostatics
We have now completed our theoretical investigation of electrostatics and magnetostatics. Our next task is to incorporate time variation into our analysis. However, before we start this let us briefly review our progress so far. We have found that the electric fields generated by stationary charges and the magnetic fields generated by steady currents are describable in terms of four field equations:
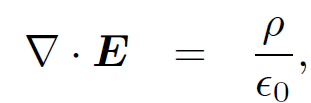 (1.1a)
(1.1a)
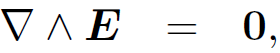 (1.1b)
(1.1b)
 (1.1c)
(1.1c)
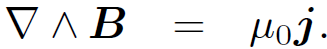 (1.1d)
(1.1d)
The boundary conditions are that the fields are zero at infinity, assuming that the generating charges and currents are localized to some region in space. According to Helmholtz's theorem the above field equations, plus the boundary conditions, are sufficient to uniquely specify the electric and magnetic fields. The physical significance of this is that divergence and curl are the only rotationally invariant differential properties of a general vector field; i.e., the only quantities which do not change when the axes are rotated. Since physics does not depend on the orientation of the axes (which is, after all, quite arbitrary) divergence and curl are the only quantities which can appear in field equations which claim to describe physical phenomena. The field equations can be integrated to give:
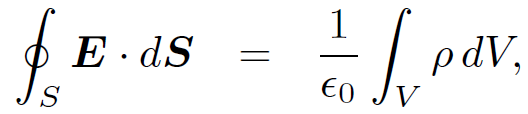 (1.2a)
(1.2a)
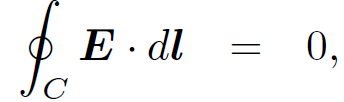 (1.2b)
(1.2b)
 (1.2c)
(1.2c)
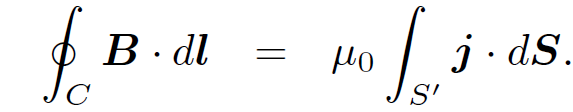 (1.2d)
(1.2d)
Here, S is a closed surface enclosing a volume V . Also, C is a closed loop, and Sʹ is some surface attached to this loop. The field equations (1.1) can be deduced from Eqs. (1.2) using Gauss' theorem and Stokes' theorem. Equation (1.2a) is called Gauss' law and says that the flux of the electric field out of a closed surface is proportional to the enclosed electric charge. Equation (1.2c) has no particular name and says that there are no such things as magnetic monopoles. Equation (1.2d) is called Ampere's law and says that the line integral of the magnetic field around any closed loop is proportional to the flux of the current through the loop. Equations (1.2b) and (1.2d) are incomplete; each acquires an extra term on the right-hand side in time dependent situations. The field equation (1.1b) is automatically satisfied if we write
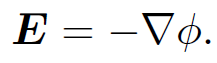 (1.3)
(1.3)
Likewise, the field equation (1.1c) is automatically satisfied if we write
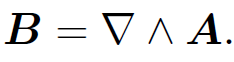 (1.4)
(1.4)
Here, ϕ is the electric scalar potential and A is the magnetic vector potential. The electric field is clearly unchanged if we add a constant to the scalar potential:
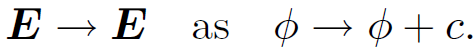 (1.5)
(1.5)
The magnetic field is similarly unchanged if we add the gradient of a scalar field to the vector potential:
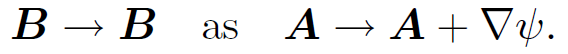 (1.6)
(1.6)
The above transformations, which leave the E and B fields invariant, are called gauge transformations. We are free to choose c and ψ to be whatever we like; i.e., we are free to choose the gauge. The most sensible gauge is the one which make our equations as simple and symmetric as possible. This corresponds to the choice
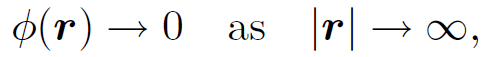 (1.7)
(1.7)
and
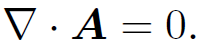 (1.8)
(1.8)
The latter convention is known as the Coulomb gauge. Taking the divergence of Eq. (1.3) and the curl of Eq. (1.4), and making use of the Coulomb gauge, we find that the four field equations (1.1) can be reduced to Poisson's equation written four times over:
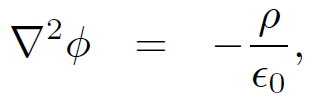 (1.9a)
(1.9a)
 (1.9b)
(1.9b)
Poisson's equation is just about the simplest rotationally invariant partial differential equation it is possible to write. Note that ∇2 is clearly rotationally invariant since it is the divergence of a gradient, and both divergence and gradient are rotationally invariant. We can always construct the solution to Poisson's equation, given the boundary conditions. Furthermore, we have a uniqueness theorem which tells us that our solution is the only possible solution. Physically, this means that there is only one electric and magnetic field which is consistent with a given set of stationary charges and steady currents. This sounds like an obvious, almost trivial, statement. But there are many areas of physics (for instance, fluid mechanics and plasma physics) where we also believe, for physical reasons, that for a given set of boundary conditions the solution should be unique. The problem is that in most cases when we reduce the problem to a partial differential equation we end up with something far nastier than Poisson's equation. In general, we cannot solve this equation. In fact, we usually cannot even prove that it possess a solution for general boundary conditions, let alone that the solution is unique. So, we are very fortunate indeed that in electrostatics and magnetostatics the problem boils down to solving a nice partial differential equation. When you hear people say things like ''electromagnetism is the best understood theory in physics" what they are really saying is that the partial differential equations which crop up in this theory are soluble and have nice properties. Poisson's equation
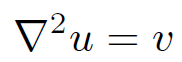 (1.10)
(1.10)
is linear, which means that its solutions are superposable. We can exploit this fact to construct a general solution to this equation. Suppose that we can find the solution to
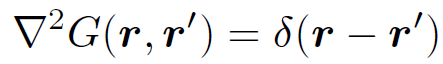 (1.11)
(1.11)
which satisfies the boundary conditions. This is the solution driven by a unit amplitude point source located at position vector rʹ. Since any general source can be built up out of a weighted sum of point sources it follows that a general solution to Poisson's equation can be built up out of a weighted superposition of point source solutions. Mathematically, we can write
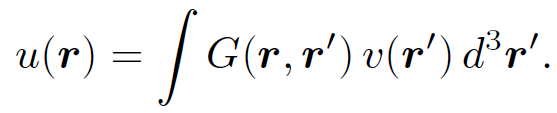 (1.12)
(1.12)
The function G is called the Green's function. The Green's function for Poisson's equation is
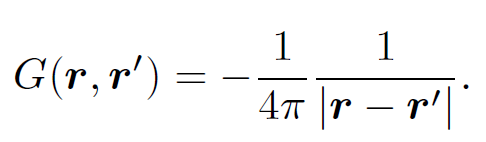 (1.13)
(1.13)
Note that this Green's function is proportional to the scalar potential of a point charge located at rʹ; this is hardly surprising given the definition of a Green's function and Eq. (1.1a). According to Eqs. (1.9), (1.10), (1.12), and (1.13), the scalar and vector potentials generated by a set of stationary charges and steady currents take the form
 (1.14a)
(1.14a)
 (1.14b)
(1.14b)
Making use of Eqs. (1.4) and (1.3) we obtain the fundamental force laws for electric and magnetic fields. Coulomb's law
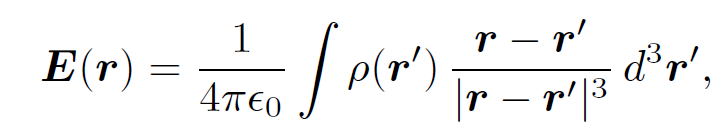 (1.15)
(1.15)
and the Biot-Savart law
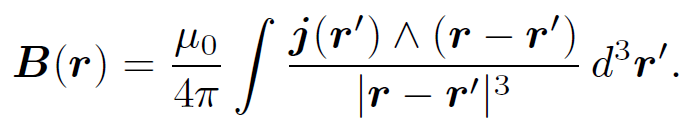 (1.16)
(1.16)
Of course, both of these laws are examples of action at a distance laws and, therefore, violate relativity. However, this is not a problem as long as we restrict ourselves to fields generated by time independent charge and current distributions. The question, now, is how badly is this scheme we have just worked out going to be disrupted when we take time variation into account. The answer, somewhat surprisingly, is by very little indeed. So, in Eqs. (1.1)-(1.16) we can already discern the basic outline of classical electromagnetism. Let us continue our investigation.



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|